Méthode des éléments finis à schéma explicite

 

 

Cette méthode est particulièrement bien adaptée à la simulation numérique des crashs et des chocs rapides d'une durée inférieure à la seconde.

Elles utilisent:

Une discrétisation spatiale par éléments finis à intégration réduite et à matrice de masses diagonales,

Une discrétisation temporelle à schéma explicite, aux différences centrées :

 

tn-1

tn+1

ou mieux

tn-1/2

tn+1/2

par rapport à t',

 

Et deux boucles de résolution seulement par rapport aux logiciels à schéma implicite:

-Une boucle externe de réactualisation géométrique,

-Une boucle interne de réactualisation matériau,

-Parfois une boucle supplémentaire pour réactualiser des conditions aux limites ou des conditions de contact.

 

Stabilité numérique

Les méthodes à schéma explicite sont conditionnellement stables dans le temps et doivent être utilisées avec un pas de temps inférieur à un pas limite, dit de stabilité, calculé à partir de la dimension de l'élément fini d et de la vitesse de propagation du son C dans le matériau:

dt < dtlimite = d/C

 

Elles correspondent généralement à un pas de temps dt compris entre 1 et 20 µsecondes et donc à un grand nombre de cycles de calcul.

 

 

Application de ce schéma d'intégration explicite sur un exemple du type masse-ressort

Un système vibrant masse-ressort se compose dune masse m, d'un ressort de constante de raideur k et d'une charge externe F(t).

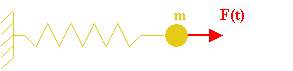
Soit l'équation différentielle du second ordre qui traduit l'équilibre dynamique du système:

 

mx''+kx=F(t) (1ddl)

 

 

et soit un axe de temps discrétisé :

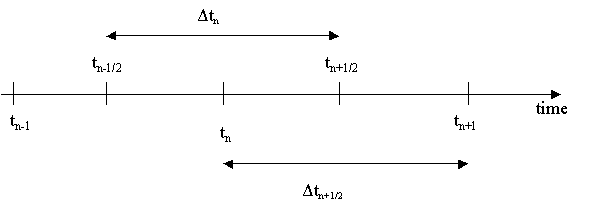
On suppose que x_n et x'_n-1/2 sont connus et on recherche x_n+1 et x'_n+1/2.

 

L'équilibre dynamique à l'instant tn s'écrit :

m.x''_n=F_n-k.x_n

 

A présent, on connaît tous les termes du membre de droite et on cherche à résoudre le système à l'aide de la méthode des différences centrées pour déterminer x''_n

x''_n = m^-1 (F_n-k.x_n)

 

x'_n+1/2 = x'_n-1/2 + dt_n.x''_n

 

 

x_n+1 = x_n + dt_n+1/2 . x'_n+1/2

 

 

Ce schéma est valable pour un pas de temps tel que dt_n < (2.m/k)^1/2

 

où m est la masse modale, k la raideur modale.

 

Ce schéma est alors dit conditionnellement stable.

Le pas d'intégration sera périodiquement réactualisé afin de vérifier la condition de stabilité numérique.