Décrivons l'algorithme du simplexe sur notre exemple.
Rappel : Programme linéaire du problème de production
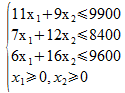
Il faut tout d'abord une solution de base admissible initiale. Dans notre cas une solution s'impose, on prend x1 = x2 = 0, on obtient la solution (0, 0, 9 900, 8 400, 9 600) et F = 0.
Géométriquement elle correspond au point origine O (0, 0).
Cela partitionne les variables en deux groupes : les variables de base (les variables non nulles), y1, y2 et y3, et les variables hors base (les variables nulles), x1 et x2.
On convient de représenter la situation par un tableau :
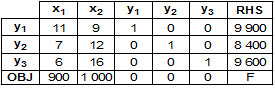
Initialement et à chaque étape le tableau s'interprète comme indiqué ci dessous :
La première ligne contient toutes les variables du problème, les 3 lignes suivantes correspondent aux 3 équations du PLFS et la dernière ligne est l'expression de la fonction à optimiser avec en dernière case F – v où v est la valeur de F au point correspondant. La première colonne contient les 3 variables de base dont les valeurs sont données par les 3 nombres correspondant dans la dernière colonne.
On peut augmenter F en augmentant x1 ou x2, prenons x2 car il a le plus grand coefficient dans F (ceci n'est pas obligatoire mais il faut bien un critère de choix), les contraintes nous imposent 9x2 ≤ 9 900, 12x2 ≤ 8 400 et 16x2 ≤ 9 600 soit x2 ≤ 1 100, x2 ≤ 700 et x2 ≤ 600.
L'augmentation maximale possible de x2 est donc de 600, elle correspond à la variable y3 qui va donc devenir nulle car on a 6x1 + 16x2 + y3 = 9 600 avec x1 = 0 et x2 = 600. On dit que x2 est la variable entrante et y3 est la variable sortante ou bien que x2 rentre dans la base et que y3 en sort, x2 devient variable de base et y3 devient variable hors base.
Les calculs à effectuer font intervenir comme nombre clé : l'élément du tableau initial situé à l'intersection de la deuxième colonne (celle de x2) et de la troisième ligne (celle de y3), cet élément est appelé le pivot. Le pivot est donc égal à 16.
Le pivotage consiste à réécrire les équations, les lignes du tableau, en remplaçant x2 par l'expression correspondant à la troisième ligne du tableau :
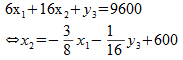
Les calculs donnent :
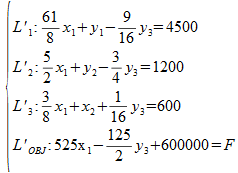
En fait les calculs effectués correspondent algébriquement à :
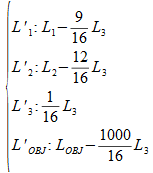
Li représente la ligne i du tableau de départ et L'i la ligne i du tableau résultat du pivotage, les coefficients au numérateur correspondent à la colonne de x2, le pivot est 16.
Nous obtenons alors le deuxième tableau :
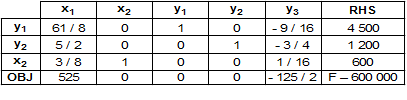
Ce tableau correspond à la solution de base admissible (0, 600, 4 500, 1200, 0), le bénéfice est F = 600 000, la machine M3 est saturée (y3 = 0) et géométriquement on est au point A1(0, 600).
Utilisons maintenant l'applet ci-dessous pour voir les itérations suivantes :
Méthode :
Récapitulons la méthode du simplexe pour un problème de maximisation :
Déterminer une solution de base admissible.
Formuler le tableau simplexe correspondant.
Si aucune variable hors base n'a un coût réduit strictement positif alors la solution courante est optimale, sinon choisir l'une de ces variables hors base (par exemple, en utilisant le critère proposé par Dantzig, celle qui a le plus grand coût réduit) pour la faire entrer en base (on parlera de variable entrante).
Si dans la colonne correspondant à la variable entrante toutes les variables de base ont un coefficient négatif ou nul alors il n'existe pas de solution optimale finie (aucune contrainte ne limite l'augmentation de la valeur de la variable entrante et en conséquence la valeur de la fonction objectif n'est pas bornée). Dans le cas contraire sélectionner la variable de base correspondant à la première contrainte bloquante (on parlera de variable sortante). Le coefficient du tableau simplexe situé à l'intersection de la colonne correspondant à la variable entrante et de la ligne correspondant à la variable sortante servira de pivot pour l'étape suivante.
Calculer le tableau simplexe suivant par pivotage et retourner à l'étape 3.
Dans le cas d'un problème de minimisation, l'étape 3 est remplacée par l'étape ci-dessous :
Si aucune variable hors base n'a un coût réduit strictement négatif alors la solution courante est optimale, sinon choisir l'une de ces variables hors base (par exemple, en utilisant le critère proposé par Dantzig, celle qui a le plus petit coût réduit) pour la faire entrer en base (on parlera de variable entrante).
