Ch.8 L'Expérimentation Statistique

PDF

Vidéo

Calculatrice

Statistiques > Ch.1: Probabilités et Variables Aléatoires Ch.2: La Loi Normale Ch.3: Le Contrôle Statistique Ch.4: L'Estimation Statistique Ch.5: Comparaisons Statistiques Ch.6: Faits et Modèles Ch.7: La Régression Linéaire Ch.8: L'Expérimentation Statistique

L'Expérimentation Statistique

Imaginons le cas suivant: un fabricant d’ampoules électriques ayant le choix entre 4 types de filaments se propose d’étudier l’influence de la nature du filament sur la durée de vie des ampoules fabriquées. Pour ce faire, il va faire fabriquer 4 échantillons d’ampoules identiques, sauf en ce qui concerne le filament, faire brûler les ampoules jusqu’à extinction, puis comparer les résultats obtenus. La technique statistique permettant cette comparaison est appelée l’analyse de la variance. Elle se présente comme une technique d’analyse de l’influence d’une variable qualitative appelée facteur (ici, le facteur "filament") sur une variable quantitative (ici, la durée de vie des lampes). L’objectif du chapitre est de présenter cette technique dans le cas de l’influence d’un facteur, puis de plusieurs facteurs.

1 - Analyse de la variance à un facteur

Recherche de l'influence d'un facteur

Nous noterons A le facteur et appellerons A₁,..., A_j,... A_p ses p modalités. Le problème est l’étude de l’influence du facteur A sur la variable quantitative Y. L’expérimentation disponible a consisté à réaliser, pour chaque modalité A_j du facteur, un certain nombre n_j de mesures de la variable Y étudiée: y_1j,..., y_ij,..., y_nij.

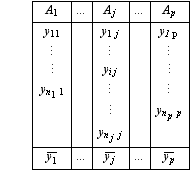
La relation d'analyse de la variance

Appelons y₁^-,..., y_j^-,..., y_p^- les moyennes des colonnes y_j^- = 1/n_j ∑_i=1^n_jy_ij, et appelons y^- la moyenne générale des mesures y^- = 1/n ∑_j=1^p ∑_i=1^n_j y_ij avec n= ∑_j=1^p n_j.

Effectuons alors la décomposition:

(yij-y-) = (yj--y-) + (yij-yj-)

En élevant au carré et en sommant, le double produit est nul. En effet:

2 ∑j=1p ∑i=1nj (yj--y-) + (yij-yj-) = 2∑j=1p (yj--y-) ∑i=1nj (yij-yj-) = 0

par définition des moyennes y_j^-.

On obtient donc:

∑j=1p ∑i=1nj (yij-y-)² = ∑j=1p nj (yj--y-)² + ∑j=1p ∑i=1n j (yij-yj-)²

relation appelée d’analyse de la variance, qui décompose la somme des carrés totale:

SCT = ∑j=1p ∑i=1nj (yij-y-)²

en une somme des carrés mesurant la variabilité intercolonnes (c’est-à-dire l’influence du facteur):

SCA = ∑j=1p nj (yj--y-)²

et une somme des carrés mesurant la variabilité intracolonnes (somme des carrés résiduelle):

SCR = ∑j=1p ∑i=1nj (yij-yj-)²

Notons la grande généralité de cette relation puisqu’elle a été établie sans faire aucune hypothèse sur les données. Cependant, la structure de la relation de base: (y_ij-y^-) = (y_j^--y^-) + (y_ij-y_j^-) revient à admettre implicitement l’additivité de l’influence du facteur (y_j^--y^-) et d’un résidu (y_ij-y_j^-).

Le modèle

Pour permettre l’inférence statistique, il est nécessaire de poser un certain nombre d’hypothèses. Le modèle de base de l’analyse de la variance s’écrit:

yij = μ + αj + εij

Les α_j sont des quantités inconnues, mais certaines, qui mesurent l’influence du facteur A. Pour lever leur indétermination à une constante près, on a l’habitude de poser:

∑j=1p njαj = 0

Les ε_ij représentent les fluctuations aléatoires correspondant aux erreurs de mesure ou à l’influence des facteurs non contôlés. Nous poserons qu’il n’y a pas d’erreur systématique, ou qu’elle est contenue dans μ, donc que E(ε_ij) = 0.

Les hypothèses suivantes stipulent que les ε_ij:

• sont indépendants: σ(ε_ij, ε_i'j') = 0 pour (i, j) ≠ (i', j'),
• ont même variance: σ²(ε_ij) = σ²,
• suivent des lois normales.

La plus restrictive, parmi ces hypothèses, est certainement la seconde d’après laquelle l’erreur sur la variable Y est indépendante de la valeur prise par Y, c’est-à-dire notamment, qu’elle n’est pas de type multiplicatif. Pour vérifier si elle est légitime, on dispose de plusieurs tests dont le plus connu est celui de Bartlett.

Test d'analyse de la variance

Il s’agit de tester si l’influence du facteur A sur la variable Y, est significative. Si le facteur A n’a pas d’influence, c’est que: α₁=...=α_j=...=α_p=0. Et, en faisant l’hypothèse qu’il en est ainsi, on peut montrer que SCA/σ² suit une loi du χ² à (p-1) degrés de liberté. Comme, d’autre part, la quantité SCR/σ² suit une loi du χ² à (n-p) degrés de liberté, il en résulte que la quantité:

f= SCA/(p-1) / SCR/(n-p)

suit une loi de Snedecor à (p-1) et (n-p) degrés de liberté.

Si la valeur f calculée est supérieure au seuil f_α lu dans la table de Snedecor, on concluera à l’influence du facteur A. Si elle est inférieure, l’information disponible ne permet pas de conclure à une influence du facteur A. Il importera d’effectuer un test à droite. En effet, les faibles valeurs de f correspondent à des différences faibles entre les moyennes y_j^- des colonnes, alors que le test vise à mettre en évidence des différences fortes.

Calcul pratique

On calcule:

SCT = ∑j=1p ∑i=1nj (yij-y-)² = ∑j=1p ∑i=1nj yij² - ny-²

SCA = ∑j=1p nj (yj--y-)² = ∑j=1p nj yj-² - ny-²

et enfin par différence:

SCR = SCT - SCA

Test de linéarité d'une régression

Ce test concerne les problèmes de régression qui ont fait l’objet du chapitre 7, mais il est plus facile de le présenter si les résultats de l’analyse de la variance sont connus.

Nous avons supposé dans ce chapitre que la ligne de régression E[Y(x)] = f(x) était une droite.

Si l’expérimentation a été menée de telle sorte que, pour chaque valeur de la variable explicative X, on dispose de q mesures de la variable expliquée Y, il est possible de tester la linéarité de la régression.

En fait, il n’est pas nécessaire qu’il y ait le même nombre q de mesures pour chaque valeur de X, mais seulement qu’il y en ait plusieurs. Nous nous placerons toutefois ici dans ce cas particulier. On dispose donc du tableau des observations ci-dessous, qui a la même structure que celui d’une analyse de la variance.

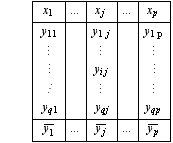
Le principe du test de linéarité consiste à s’assurer que les moyennes y_j^- ne sont pas " trop éloignées " de la droite de régression.

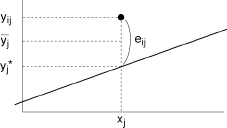
Le déroulement en est le suivant. Soit:

yj* = axj+b

le point d’abcisse x_j de la droite des moindres carrés et soit:

eij = (yij - yj*)

le résidu correspondant à l’observation y_ij. On peut décomposer e_ij en:

eij = (yj--yj*) + (yij-yj-)

En élevant au carré et en sommant sur i et j, le double produit est nul et on obtient:

∑j=1p ∑i=1q (yij-yj*)² = q ∑j=1p (yj--yj*)² + ∑j=1p ∑i=1q (yij-yj-) 2

Soit S₁² le premier terme de la décomposition:

S1² =q ∑j=1p (yj- - yj*)²

qui est appelé le défaut d’ajustement.

Et soit S₂² le second terme:

S2² = ∑j=1p ∑i=1q (yij - yj-)²

Si on a bien affaire à une régression linéaire, S₁²/σ² suit une loi du χ² à (p-2) degrés de liberté. Comme d’autre part, S₂²/σ² suit une loi du χ² à q(p-1) degrés de liberté, et que S₁² et S₂² sont indépendantes (puisque chaque y_j^- est indépendant de ∑_i=1^q (y_ij - y_j^-)²), il en résulte que le quotient:

f = S1²/p-2 / S2²/q(p-1)

suit une loi de Snedecor à (p-2) et q (p-1) degrés de liberté. Cette propriété permet de tester la linéarité. Ici encore, c’est un test à droite qu’il faut faire, puisque ce que l’on veut éventuellement montrer c’est une valeur élevée du défaut d’ajustement.

2 - Etude de l'influence de deux facteurs

Imaginons que le fabricant d’ampoules évoqué plus haut, se préoccupe d’étudier l’influence, sur la durée de vie des ampoules, non seulement du type de filament utilisé, mais également de la nature du gaz de remplissage.

Il pourrait évidemment faire, d’une part, une première étude " filament " en utilisant l’analyse de la variance à un facteur, puis procéder, d’autre part, à une étude " gaz " en tous points analogue. Cela fait, il lui resterait à rapprocher les résultats de ces deux études pour se faire une idée de l’influence des deux facteurs étudiés. Mais en procédant de la sorte, il postulera implicitement l’additivité des influences " filament " et " gaz ", ce qui n’est pas acquis.

L’analyse de la variance à deux facteurs va permettre de traiter globalement le problème, et de mettre en évidence, éventuellement, ce qu’il est convenu d’appeler les interactions des facteurs étudiés.

Plan factoriel

Soit, d’une façon générale, A et B les deux facteurs dont on se propose d’étudier l’influence sur une variable quantitative Y. Nous appellerons A₁,..., A_i,..., A_p les p modalités du facteur A, et B₁,..., B_j,..., B_q les q modalités du facteur B. La mise en oeuvre de l’analyse de la variance à deux facteurs nécessite de disposer d’au moins une mesure de Y pour toute combinaison (A_i, B_j) des modalités des facteurs.

Nous admettrons que l’expérimentation a permis de réaliser r répétitions, c’est-à-dire r mesures pour chacune des p q combinaisons des modalités des facteurs. Le cas où il n’y a pas de répétitions (r=1) fera l’objet d’un paragraphe particulier.

Les essais sont donc menés de façon à obtenir le tableau de mesures ci-dessous, une des difficultés de l’expérimentation étant d’éviter les mesures manquantes.

Le plan d’expérience ainsi réalisé est appelé plan factoriel. Il est dit équilibré parce qu’il y a le même nombre de mesures dans chaque ligne et dans chaque colonne. Il existe d’autres plans d’expérience équilibrés qui évitent le principal inconvénient du plan factoriel, qui est d’être très coûteux du point de vue du nombre de mesures à effectuer.

Modèle additif et modèle avec interaction

Le modèle le plus général, en admettant l’additivité des erreurs ε_ijk, est le suivant:

yijk = μij + εijk

En explicitant μ_ij, un modèle couramment utilisé est le modèle additif:

μij = μ + αi + βj

On suppose ainsi qu’il y a additivité des effets: l’action conjuguée des modalités A_i et B_j est la somme des actions isolées de A_i d’une part et de B_j d’autre part. Si l’on ne suppose pas réalisée cette hypothèse restrictive d’additivité, on adopte le modèle avec interaction:

μij = μ + αi + βj + γij

Il n’y a plus additivité des effets car, aux actions directes de A_i et B_j, s’ajoute le terme γ_ij qui traduit un effet supplémentaire dû à la conjonction des modalités A_i et B_j.

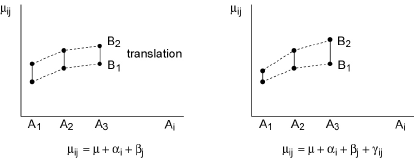
On dit que (α₁,..., α_p) et (β₁,..., β_q) sont les actions des facteurs A et B, tandis que (γ₁₁,..., γ_pq) sont les interactions du couple (A, B). On peut encore dire que le modèle avec interaction traduit le fait que l’action du facteur A, par exemple, dépend des modalités du facteur B, comme l’illustrent les figures ci-dessus.

Pour lever l’indétermination de μ, on pose les relations suivantes:

∑i=1p αi = ∑j=1q βj = ∑i=1p γij = ∑j=1q γij = 0

Relation d'analyse de la variance

Appelons y_i^- la moyenne d’une colonne du tableau des mesures: y_i^- = 1/qr ∑_jk y_ijk.

Appelons y_j^- la moyenne d’une ligne du tableau: y_j^- = 1/pr ∑_ik y_ijk.

Appelons y_ij^- la moyenne d’une case du tableau: y_ij^- = 1/r ∑_k y_ijk.

Appelons enfin y^- la moyenne générale des mesures: y^- = 1/pqr ∑_ijk y_ijk.

Effectuons alors la décomposition:

(yijk-y-) = (yi--y-)+(yj--y-)+[(yij--y-)-(yi--y-)-(yj--y-)]+(yijk - yij-)

En élevant au carré et en sommant, les doubles produits s’annulent par définition des différentes moyennes, à la condition stricte que le tableau soit complet, c’est-à-dire qu’il n’y ait aucune mesure manquante. On obtient par conséquent:

∑ijk(yijk-y-)² = qr∑i(yi--y-)² + pr∑j(yj--y-)² + r∑ij[(yij--y-)-(yi--y-)-(yj--y-)]² + ∑ijk(yijk-yij-)²

que nous noterons symboliquement:

SCT = SCA + SCB + SCAB + SCR

C’est la relation d’analyse de la variance. Elle permet de décomposer la somme des carrés totale en quatre sommes. Les deux premières correspondent respectivement aux actions de A et de B. La troisième correspond à l’interaction de A et B. La dernière est la somme des carrés résiduelle.

Les tests d'analyse de la variance

Admettons, comme dans le cas d’un seul facteur, que les ε_ijk sont des variables aléatoires centrées, de même variance σ², indépendantes, et qu’elles suivent des lois normales. Il est alors possible d’effectuer une inférence statistique à partir des observations, et de tester:

• la présence d’une interaction,
• l’influence d’un facteur.

1. Test de l'interaction

   Faisons l’hypothèse qu’il n’y a pas d’interaction des facteurs A et B, c’est-à-dire que:

   ∀ i,j: γij = 0

   On montre que, s’il en est ainsi, la quantité SCA/ σ² suit une loi du χ² à (p-1)(q-1) degrés de liberté.

   Comme d’autre part, la quantité SCR/σ² suit une loi du χ² à (n-p q) = p q (r-1) degrés de liberté, il en résulte que le quotient:

   fAB = SCAB/(p-1)(q-1) / SCR/(pq(r-1))

   suit une loi de Snedecor à (p-1)(q-1) et p q (r-1) degrés de liberté, s’il n’y a pas d’interaction.

2. Test de l'influence d'un facteur

   Faisons l’hypothèse que le facteur A, par exemple, n’a pas d’influence sur la variable Y. On montre alors que la quantité SCA/σ² suit une loi du χ² à (p-1) degrés de liberté.

   Par conséquent, la quantité:

   fA = SCA/(p-1) / SCR/(pq(r-1))

   suit une loi de Snedecor à (p-1) et p q (r-1) degrés de liberté.

3. Exécution des calculs

   On calcule SCA, SCB, SCAB et SCR par les formules suivantes:

   SCA = qr∑i yi-² - pqr y-²

   SCB = pr∑j yj-² - pqr y-²

   SCAB = r∑ij yij-² - pqr y-² -SCA-SCB

   SCT = ∑ijk yijk² - pqr y-²

   Puis SCR s’obtient par différence:

   SCR = SCT - SCA - SCB - SCAB

   On dresse enfin le tableau:

   

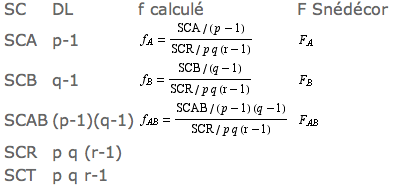
Analyse de la variance sans répétitions

Supposons qu’on n’ait réalisé qu’une seule mesure y_ij pour chaque couple de modalités (A_i, B_j), conformément au tableau ci-dessous.

L’équation d’analyse de la variance s’écrit alors:

∑ij (yij-y-)² = qr∑i (yi--y-)² + pr∑j (yj--y-)² + r∑ij [(yij-y-) - (yi--y-) - (yj--y-)]²

soit, avec les notations habituelles:

SCT = SCA + SCB + SCAB

Il devient impossible de tester l’interaction, puisqu’on ne dispose plus d’une quantité telle que SCR permettant, par division, d’éliminer σ² et d’obtenir une loi de Snedecor. Il est donc nécessaire, dans ce cas de faire l’hypothèse (impossible à vérifier) qu’il n’y a pas d’interaction. On doit donc adopter le modèle additif:

yij = μ + αi + βj + εij

Sous cette condition, et quelles que soient les actions des facteurs A et B, on montre, comme dans le cas général, que SCAB/σ² suit une loi du χ² à (p-1)(q-1) degrés de liberté.

Dès lors, pour tester l’influence de A, par exemple, faisons l’hypothèse que les α_i sont tous nuls. Elle entraine que SCA/σ² suit une loi du χ² à (p-1) degrés de liberté et, par conséquent, que la quantité:

fA = SCA/(p-1) / SCAB/((p-1)(q-1))

suit une loi de Snedecor à (p-1) et (p-1) (q-1) degrés de liberté.

Exercices

Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !

Exercice 1

Les données suivantes représentent l’effet du temps T (en heures), sur la perte H (en ppm) de l’hydrogène contenu dans des échantillons d’acier à 20 degrés centigrades.

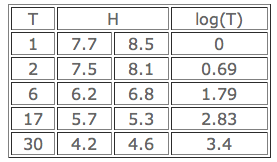
1. Le facteur temps a-t-il une influence sur la perte en hydrogène ?
2. Peut-on admettre que la relation entre H et T est de la forme H = α + β log(T) ?

Avec y = H et x = log(T), on donne:

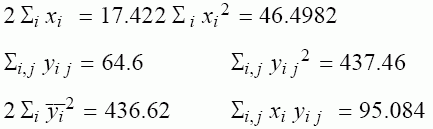
Il s'agit d'une application classique de l'analyse de la variance dans la recherche expérimentale :
- tel facteur (ici le temps) a-t-il une influence sur tel phénomène (ici la perte en hydrogène)
- si oui, quantifier cette influence.

a) On complète le tableau de la façon suivante :

T	H
1 2 6 17 30	7.7 8.5 7.5 8.1 6.2 6.8 5.7 5.3 4.2 4.6	8.1 7.8 6.5 5.5 4.4

Les moyennes sont-elles significativement différentes ?

SCT==-=437.46-=20.144

SCA==-=436.62-=19.304

SCR=SCT-SCA=0.804

On dresse alors le tableau suivant :

Sources de variation	SC	DDL	Var estimée	f calculé	F Snédécor
Temps	19.304	4	4.826	28.72	5% 1% 1‰ 5.19 11.4 31
Résiduelle	0.840	5	0.168

L'influence du temps est significative au risque 1% de se tromper (de conclure à une différence alors qu'il n'y en a pas).

b) Le graphique H=f(T) donne (avec Mathematica)

Liaison non linéaire : on envisage une transformation en log(T) (empirique au vu de l'allure de la fonction, ou mieux pour raison théorique). Ca semble devenu assez linéaire, mais il faut s'en assurer par un test.

Avec les notations du polycopié :

==0.84, le SCR calculé précédemment.

=-

Mais : = SCR en régression linéaire = (1-)SCT.

Or :

==

num=-2×5 =-2×5× ×

num=95.084-=-17.4492

(-)=2 [-]=46.4982-=16.15256

=-10×=437.46-=20.144=SCT

⇒ ==0.93576

⇒ =(1-)SCT=1.294

⇒ =1.294-0.84=0.454

⇒ f==0.9<1, tout à fait admissible.

f étant inférieur à 1, il est inutile d'allez voir dans la table. On accepte l'hypothèse de linéarité.

Exercice 2

Un laboratoire utilise 4 thermomètres de façon interchangeable pour faire des mesures de température. Pour étudier si les résultats diffèrent suivant les thermomètres, ces derniers ont été placés dans un récipient maintenu à température constante. Trois lectures ont été faites avec chaque thermomètres. Les résultats en degrés centigrades ont été les suivants:

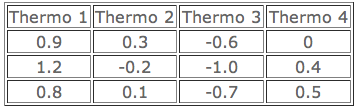
Que peut-on en conclure ? On donne:

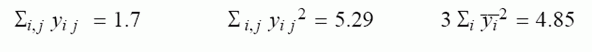
Il s'agit d'un classique d'utilisation de l'analyse de la variance à la métrologie : y a t-il des différences à craindre suivant le thermomètre qui sera utilisé pour la mesure ? L'objectif est d'apprendre à bien organiser les calculs.

On calcule d'abord :

SCT==-=5.29-=5.04

SCA==-=4.85-=4.6

On obtient alors, par différence :

SCR=SCT-SCA=5.049-4.609=0.44

On établit alors le tableau su!ivant :

Sources de variation	SC	DDL	Var estimée	f calculé	F Snédécor
Facteur thermomètre	SCA=4.609	p-1=3			5% 1% 1‰ 4.07 7.59 15.8
Résiduelle	SCR=0.44	n-p=8

Bien faire remarquer qu'on fait un test à droite parce que ce l'on veut tester c'est > : la variabilité due au facteur étudié est plus grande que celle qui serait dur à l'intervention du hasard seul.

Avec un risque plus petit que 1‰ de se tromper, on peut conclure que le facteur "thermomètre" est source d'hétérogénéité.

Exercice 3

Le modèle y_ij = μ + α_i + ε_ij, où les α_i sont des quantités inconnues mais déterminées, est appelé modèle à effets fixes. Un autre modèle est le celui qui est appelé à effets aléatoires et qui s’écrit y_ij = μ + a_i + b_ij où a_i est une réalisation d’une variable aléatoire A avec E(A) = 0 et b_ij est une réalisation d’une variable aléatoire B avec E(B) = 0. Les variables A et B sont caractérisées par leurs variances σ A₂ et σ B₂ et sont indépendantes. L’exemple suivant est une application de ce dernier modèle.

Un ciment est caractérisé par sa résistance à la compression (mesurée sur des prismes de béton fabriqués à partir d’un échantillon du ciment). Pour étudier la variabilité des productions journalières d’un four à ciment, on a réalisé deux mesures sur des échantillons prélevés chaque jour pendant une période de 10 jours. On a obtenu les résultats ci-après.

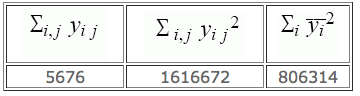
1. Estimer la variance des mesures et la variance des productions.
2. Sont-elles différentes ? Conclure.
3. On donne ∑ i (y_i ⁢ 1 - y_i ⁢ 2)² =9126. Rapprocher ce résultat de ceux de l’analyse de la variance.

Exercice 4

Les produits appelés " cru ", à l’entrée d’un four de cimenterie, sont ajustés en tenant compte du titre en carbonates. On veut savoir avec quelle précision est connu ce titre dans le cadre de l’usine. Le laboratoire dispose de cinq chimistes. Il y a deux batteries de dosage.

L’expérimentation a été menée dans le but de mettre en évidence une influence possible de l’opérateur ou de la batterie sur le résultat d’un dosage. Le tableau suivant indique les résultats pour 10 crus, chacun d’eux ayant fait l’objet d’une analyse par chaque opérateur et sur chaque batterie. Dans chaque case du tableau, le premier nombre correspond à la batterie n°1 et le second à la batterie n°2.

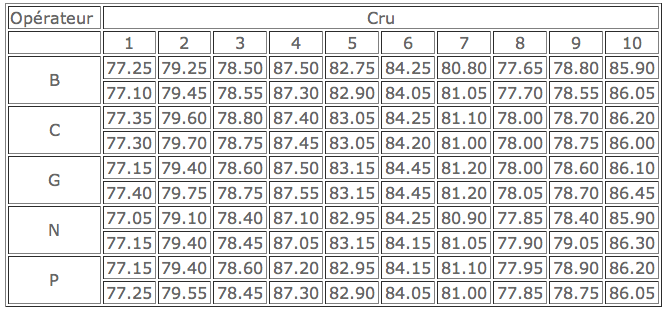
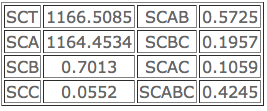
Analyser les résultats. On donne les sommes de carrés correspondants aux actions des facteurs et à leurs interactions doubles et triple:

Exercice 5

On veut connaître l’influence des facteurs de fabrication sur la qualité d’un ciment et, plus particulièrement, l’influence sur la cuisson des trois facteurs: qualité de l’alumine, température de cuisson, temps de palier de cuisson.

Les critères de cuisson sont: la teneur en alumine libre et la teneur en chaux libre des produits à la sortie du four.

Lors des essais effectués, six crus ont été testés (cru industriel témoin, cru AH 3, cru Guilini, cru A6000, cru A8000, cru A9000), à trois températures différentes (1350°, 1400°, 1450°). A chaque température, les temps de palier étaient de 10, 20 et 30 mn. On a obtenu les résultats suivants:

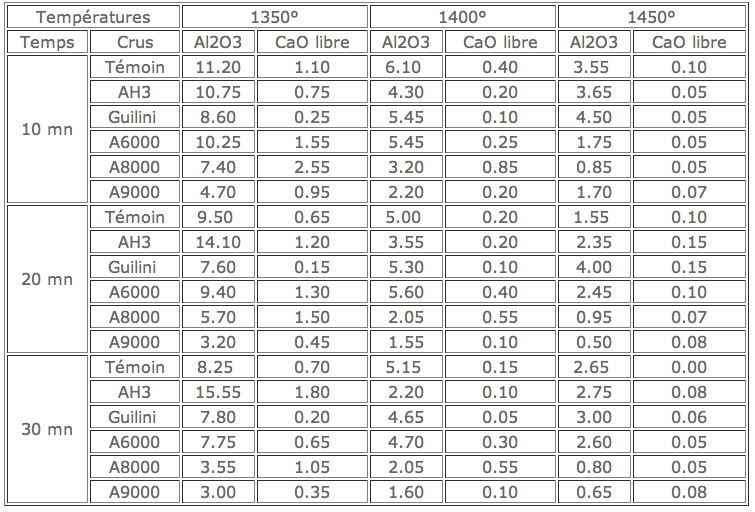
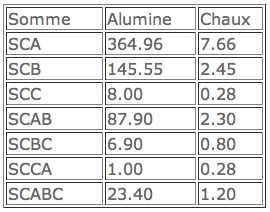
Analyser ces résultats. On donne les éléments de calcul: