La Régression Linéaire

Les sciences exactes sont fondées sur la notion de relations répétables, qui peut s’énoncer ainsi: dans les mêmes conditions, les mêmes causes produisent les mêmes effets. Notant alors x la mesure des causes, et y celle des effets, la liaison entre y et x s’écrit suivant la relation fonctionnelle y = f c (x): à une valeur donnée de x correspond une valeur bien déterminée de y.

Or, pour de nombreux phénomènes (notamment industriels), une étude exhaustive de tous les facteurs est impossible, à cause de leur grand nombre ou de leur complexité. Il en résulte que la reproductibilité des conditions, d’une expérience à une autre, ne peut être garantie. Partant de cette constatation, la statistique va permettre d’étendre la notion de relation fonctionnelle répétable, à celle de corrélation où la relation entre x et y est entachée d’une certaine dispersion due à la variabilité des conditions d’expérience: on écrira y=f(x)+ε, où ε est une variable aléatoire.

1 - La droite des moindres carrés

Nuage des individus

Le problème est d’étudier l’influence d’une variable quantitative X sur une autre variable quantitative Y. La première est souvent appelée variable explicative (ou encore exogène) et la seconde est appelée variable expliquée (ou encore endogène). Pour résoudre ce problème, on a réalisé une expérimentation qui consiste à prélever un échantillon de n individus, et à mesurer sur chacun d’eux les valeurs prises par chacune des deux variables. En vue, par exemple, d’étudier l’influence de la teneur en carbone d’un acier sur sa résistance à la traction, on a procédé à la mesure de ces deux variables sur 100 éprouvettes. On dispose donc d’un échantillon de n couples d’observations (x_i, y_i) que l’on peut représenter sur un graphique, dans le plan R², où chaque point i, d’abscisse x_i et d’ordonnée y_i, correspond à un couple d’observations. Plusieurs cas peuvent se présenter.

Les points s’alignent sur une courbe qui, dans l’hypothèse la plus simple est une droite. On dit que la relation entre Y et X est fonctionnelle: lorsque la valeur de X est donnée, celle de Y est déterminée sans ambiguïté. C’est le cas idéal qui, expérimentalement, n’est jamais réalisé de façon parfaite.

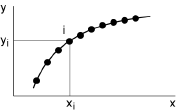
Les mesures sont en effet toujours entachées de quelque imprécision. Les points forment alors un nuage. Mais celui-ci présente une orientation qui suggère, par exemple, que lorsque X augmente, la valeur moyenne de Y augmente également.

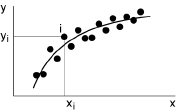
Lorsque X est donné, Y n’est pas complètement déterminé: ses valeurs se dispersent autour d’une certaine valeur moyenne. Mais les valeurs moyennes décrivent, lorsque X varie, une courbe qui est appelée la ligne de régression de Y par rapport à X:

E(Y|X=x) = f(x)

La liaison entre Y et X est alors appelée stochastique (ou statistique). Un cas particulièrement important est celui où le nuage se dispose suivant une forme allongée et exhibe une tendance sensiblement linéaire. C’est à ce cas de régression linéaire que nous allons nous attacher dans ce chapitre.

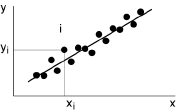
Cette condition de linéarité n’est pas aussi restrictive qu’il pourrait paraître: une transformation mathématique appropriée permettra toujours de passer d’une ligne de régression d’équation quelconque à une droite de régression. Si la tendance est, par exemple, de la forme y=b x^a, il suffira d’effectuer les changements de variable y'=log(y) et x'=log(x) pour retrouver une relation linéaire: log(y) =a log(x)+log(b).

Caractérisation de la droite de régression

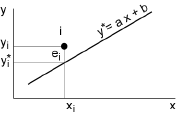
Nous cherchons une droite y*=ax+b qui décrive au mieux la tendance du nuage observé. La démarche la plus couramment utilisée consiste à:

faire l’hypothèse que, pour chaque individu i, on a: y_i = a x_i+b + e_i, où e_i est une certaine «erreur», appelée résidu, qui s’ajoute à la valeur y_i* = a x_i+b qui résulterait d’une relation fonctionnelle linéaire entre Y et X,
à rechercher la droite y*=ax+b, qui est dite droite des moindres carrés, telle que la somme quadratique des résidus e_i soit minimale, c’est-à-dire que:

S= ∑_i=1ⁿ e_i² soit minimale

Cette quantité S s’écrit en fonction de a et b: S= ∑_i=1ⁿ (y_i - a ⁢ x_i - b)². Elle est minimale si les dérivées partielles par rapport à a et b sont nulles:

∂S/∂a = -2∑_i=1ⁿ x_i(y_i-ax_i-b) = -2∑_i=1ⁿ x_ie_i = 0 (1)

∂S/∂b = -2∑_i=1ⁿ (y_i-ax_i-b) = -2∑_i=1ⁿ e_i = 0 (2)

En appelant y^- et x^- les moyennes des valeurs x_i et y_i:

y^-= 1/n ∑_i=1ⁿ y_i et x^-= 1/n ∑_i=1ⁿ x_i

l’équation (2) permet d’obtenir la valeur de l’ordonnée à l’origine de la droite:

b = y^--ax^-

ce qui signifie que la droite des moindres carrés passe par le point moyen du nuage, de coordonnées (x^-, y^-), puisque son équation devient:

y*-y^- = a(x-x^-)

Le système des deux équations (1) et (2) devient alors, en remplaçant b par sa valeur:

∑_i=1ⁿ x_i[(y_i-y^-) - a(x_i-x^-)] = 0 (3)

∑_i=1ⁿ [(y_i-y^-) - a(x_i-x^-)] = 0 (4)

Multipliant (4) par x^- et retranchant de (3), il vient:

∑_i=1ⁿ (x_i-x^-) [(y_i-y^-) - a(x_i-x^-)] = 0 (5)

d’où l’on déduit la valeur de a:

a =∑_i=1ⁿ (x_i-x^-)(y_i - y^-) / ∑_i=1ⁿ (x_i-x^-)²

On peut noter que: 1/n ∑_i=1ⁿ (x_i-x^-) (y_i - y^-) est la covariance empirique de X et Y, et que: 1/n ∑_i=1ⁿ (x_i-x^-)² est la variance empirique de X. Par conséquent, l’expression de a peut s’écrire:

a = s(X,Y)/s²(X)

Analyse de la variance

Rapportant l’observation y_i à la moyenne y^- des observations, on peut écrire:

(y_i-y^-) = a (x_i-x^-) + e_i

Dans cette expression, la quantité a (x_i-x^-) représente ce qui est « expliqué » par X, et la quantité e_i est une erreur qu’on a appellée un résidu.

En élevant au carré et en sommant pour toutes les observations, il vient:

∑_i=1ⁿ (y_i-y^-)² = a² ∑_i=1ⁿ (x_i-x^-)² + ∑_i=1ⁿ e_i² (6)

En effet, le double produit est nul puisqu’il peut s’écrire:

2a ∑_i=1ⁿ (x_i-x^-)[(y_i-y^-)-a(x_i-x^-)]

forme sous laquelle on reconnait le premier membre de l’équation (5) précédente.

La relation (6) est appelée équation d’analyse de la variance. En fait, il s’agit de sommes de carrés: il faudrait diviser par n pour obtenir des variances. La relation (6) s’écrit souvent:

SCT = SCE + SCR

Elle décompose la somme des carrés totale SCT en une somme expliquée SCE et une somme résiduelle SCR.

Coefficient de corrélation

On définit alors le carré du coefficient de corrélation noté r² comme le ratio:

r² = SCE/SCT

Il représente donc la part relative de la variabilité totale de Y qui est expliquée par X:

SCE = r² SCT

Et, symétriquement, (1- r²) représente la part résiduelle:

SCR = (1- r²) SCT (7)

En explicitant SCE et SCT puis a, on peut écrire:

Im1

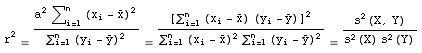
Le coefficient de corrélation a le signe de la covariance:

Im2

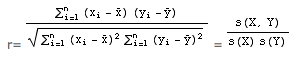
de telle façon que, si X et Y varient dans le même sens, r est positif; sinon, il est négatif.

Il résulte de la relation (7) que le coefficient de corrélation est toujours compris entre -1 et 1, puisqu’une somme de carrés est nécessairement positive.

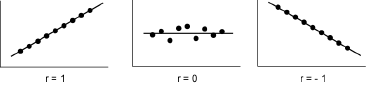
Le coefficient de corrélation présente les valeurs remarquables suivantes:

si |r| = 1, il y a une relation fonctionnelle linéaire entre X et Y;
si r = 0, Y est indépendante de X: la covariance est nulle et la droite de régression est horizontale.
la liaison entre X et Y est d’autant plus intime que |r| est voisin de 1, et d’autant plus faible que |r| est voisin de 0.

2 - Propriétés statistiques de la droite des moindres carrés

Le modèle de la régression linéaire

Nous nous sommes jusqu’ici limités à décrire l’échantillon des valeurs observées (x_i, y_i) sans faire d’hypothèses sur la structure de la population dans laquelle il a été prélevé. Pour pouvoir pratiquer l’inférence, c’est-à-dire émettre des conclusions qui soient valables pour cette population, nous sommes obligés d’adopter un modèle de population.

Nous admettrons que, pour un individu i prélevé au hasard dans la population, x_i est connu sans erreur, et que y_i est une réalisation d’une variable aléatoire: Y_i = αx_i + β + ε_i. Les paramètres α et β sont des quantités certaines, mais inconnues qu’il faudra estimer.

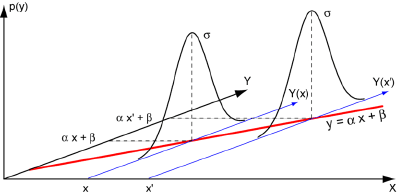
Les quantités ε_i sont des variables aléatoires avec les propriétés suivantes:

elles sont centrées: E (ε_i) = 0,
elles ont même variance: E (ε_i²) = σ²,
elles sont indépendantes: E(ε_i ε_j) = 0 si i ≠ j.

Pour une valeur donnée x_i, on a:

E [Y(x_i)] = αx_i + β

La ligne de régression est donc la droite d’équation y = αx+β. La dispersion autour de cette droite correspond à un écart-type σ: elle est indépendante de X.

Rappelons que nous avions écrit, à partir de la droite des moindres carrés que:

y_i = ax_i+b + e_i

Sous les hypothèses ci-dessus, nous allons montrer que a et b sont des estimations sans biais de α et β et qu’il est possible d’estimer σ² à partir de SCR= ∑_i=1ⁿ e_i².

Propriétés de a et b

Conformément au modèle adopté, a est à considérer comme une réalisation de la variable aléatoire:

A = ∑_i=1ⁿ (x_i-x^-)(Y_i - Y^-) / ∑_i=1ⁿ (x_i-x^-)²

et b comme une réalisation de la variable aléatoire:

B = Y^-- Ax^-

A et B sont des estimateurs sans biais et convergents de α et β. Les calculs qui permettent de le montrer, peuvent être omis mais ils constituent toutefois un bon entrainement à la pratique des opérateurs " espérance mathématique " et " variance ".

Tenant compte de ce que Y_i = αx_i + β + ε_i, on peut mettre A et B sous la forme:

A = α+∑_i=1ⁿ (x_i-x^-)(ε_i - ε^-) / ∑_i=1ⁿ (x_i-x^-)² = α+ ∑_i=1ⁿ (x_i-x^-)ε_i / ∑_i=1ⁿ (x_i-x^-)²

B = β - x^-(A-α) + ε^-

On en déduit tout d’abord les espérances mathématiques de A et B:

E(A) = α + ∑_i=1ⁿ (x_i-x^-)E(ε_i) /∑_i=1ⁿ (x_i-x^-)² = α

E(B) = β- x^- E(A-α)+E(ε^-) = β

On peut calculer ensuite les variances de A et B:

σ²(A) = ∑_i=1ⁿ (x_i-x^-²)σ²(ε_i) /[∑_i=1ⁿ (x_i-x^-)²]² = σ² / ∑_i=1ⁿ (x_i-x^-)²

σ²(B) = x^-² σ²(A)+ σ²(ε^-)-2σ(ε^-,A) = (x^-² σ²) /∑_i=1ⁿ (x_i-x^-)² + σ²/n

puisque la covariance de ε^- et A est nulle:

Im3

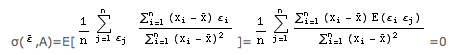
On peut enfin calculer la covariance de A et B:

σ(A,B) = E[(A-α)(B-β)] = E[(A-α)(ε^--x^-(A-α))] = σ(ε^-,A)-x^- σ²(A) = -x^-σ² / ∑_i=1ⁿ (x_i-x^-)²

On constate ainsi que A et B sont des estimateurs de α et β: sans biais (E(A)=α, E(B)=β) et convergents (σ²(A) = σ²/∑_i=1ⁿ (x_i-x^-)² tends vers 0 et σ²(B) = (x^- 2 ∑_i=1ⁿ (x_i-x^-)² + 1/n) σ² tends vers 0) mais qu’ils ne sont pas indépendants (σ (A, B) ≠ 0).

Par contre, A et Y^- sont indépendants puisque σ(ε^-,A) =0. Ce résultat sera exploité un peu plus loin.

Estimation de s²

Montrons maintenant que:

σ*² = SCR/(n-2) = ∑_i=1ⁿ e_i²/(n-2) = [(1-r²) ∑_i=1ⁿ (y_i-y^-)²] / (n-2)

est une estimation sans biais de σ². Utilisant conjointement:

(y_i-y^-) = a(x_i-x^-) + e_i
(y_i-y^-) = α(x_i-x^-) + (ε_i-ε^-)

on peut écrire que:

∑_i=1ⁿ (ε_i-ε^-)² = (a - α)² ∑_i=1ⁿ (x_i-x^-)² + ∑_i=1ⁿ e_i² +2(a-α) ∑_i=1ⁿ (x_i-x^-) e_i

On en déduit que:

E(∑_i=1ⁿ e_i²) = (n-1)σ² - σ² - 0 = (n-2)σ²

et finalement:

E(σ*²) = σ²

3 - La prévision statistique

Objectifs

Dans une entreprise, on peut distinguer trois fonctions essentielles que nous allons brièvement illustrer par des exemples.

Décision: les performances d’un matériel dépendent de son âge. Au-dessous d’un certain seuil de performance, il convient de le réformer. Etant donné l’âge d’un matériel, il faudra décider de sa réforme ou de son maintien en activité.

Prévision: la consommation en matière première (ou en énergie) dépend de la quantité produite. Visant, pour une période future, une certaine production, quel stock de matière première faut-il prévoir ?

Contrôle: dans le même contexte, une certaine production ayant été assurée pour une certaine consommation, cette dernière est-elle « normale », faible, élevée ?

Ces trois problèmes se formulent finalement de la même façon. Pour une valeur donnée de X, quelle valeur attribuer à Y, et avec quelle précision ? D’un point de vue pratique, c’est l’objectif principal de ce qui suit.

Nous chercherons à apporter des réponses aux questions suivantes:

la liaison entre les deux variables Y et X est-elle significative ? Autrement dit, peut-on ou non admettre que α = 0 ?
quels intervalles de confiance retenir pour les paramètres du modèle α et β ?
pour une valeur donnée de X, comment estimer la valeur correspondante de Y ?

Hypothèse de normalité

La résolution de ces problèmes nécessite de compléter le modèle, en admettant pour les ε_i, outre les hypothèses précédentes (variance constante, indépendance), l’hypothèse de normalité.

Cette dernière hypothèse va permettre d’établir les lois de probabilité des estimateurs A et B, et celle d’un point quelconque A x + B. En effet, les x_i étant fixés, ces trois quantités sont des combinaisons linéaires des ε_i, donc suivent elles aussi des lois normales.

On peut montrer d’autre part que, sous l’hypothèse de normalité des ε_i, la quantité: ∑_i=1ⁿ e_i² σ² suit une loi du χ² à (n - 2) degrés de liberté, et qu’elle est indépendante des quantités A et B.

Test d'indépendance des variables

La variable aléatoire A suit une loi normale dont nous avons montré en 2.2 que l'espérance était égale à α et la variance à:

σ²(A) = σ²/∑_i=1ⁿ (x_i-x^-)²

Faisons l’hypothèse qu’il n’y a pas de liaison entre les variables, c’est-à-dire que α = 0. Il en découle que A suit une loi de moyenne nulle, donc que la quantité A/σ(A) suit une loi normale centrée réduite.

Par suite, si on estime σ² par:

σ*² = [(1-r²)/(n-2)] ∑_i=1ⁿ (y_i-y^-)²

la quantité:

T= A/(σ* / √∑_i=1ⁿ (x_i-x^-)²)

suit une loi de Student à (n-2) degrés de liberté. Il suffit de calculer sa valeur expérimentale:

t= a/σ* / √∑_i=1ⁿ (x_i-x^-)²

et de la comparer au seuil lu dans la table correspondante pour le risque choisi. Les mêmes propriétés permettent de calculer un intervalle de confiance pour α.

Test de nullité de l'ordonnée à l'origine

La variable aléatoire B suit une loi normale d'espérance égale à β, ordonnée à l’origine de la droite de régression y(x) =αx+β, et nous avons montré en 2.2 que sa variance était égale à:

σ²(B) = (x^-²/∑_i=1ⁿ (x_i-x^-)² + 1/n) σ²

En procédant comme précédemment, on peut tester si la droite de régression passe par l’origine (β=0), ou calculer un intervalle de confiance pour l’estimation de β.

Intervalles de confiance pour une valeur donnée x de X

Nous allons envisager successivement les intervalles de confiance:

d’un point de la droite de régression y(x) = αx + β, c’est-à-dire de la valeur moyenne des observations pour une valeur x donnée,
puis d’un point du nuage Y(x), c’est-à-dire de la valeur d’une observation pour une valeur x donnée.

Il est absolument nécessaire de bien prendre conscience de la différence fondamentale entre ces deux problèmes, dont les applications sont nombreuses et importantes: il s’agit dans le second cas de l’intervalle de confiance de Y(x), alors que dans le premier cas il s’agit de l’intervalle de confiance de E [Y(x)].

Intervalle de confiance d'un point de la droite y=αx+β

L’équation de la droite de régression s’écrit:
```
y(x) = αx+β
```
Celle de la droite des moindres carrés s’écrit:
```
y*(x) = ax+b
```
que l’on considère comme une réalisation de la variable aléatoire
```
Y*(x) = Ax+B
```
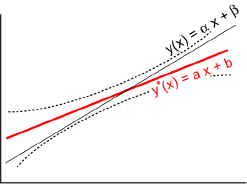
D’après les résultats établis en 2.2, E[Y*(x)] = y(x). Donc le point y*(x) de la droite des moindres carrés est une estimation du point correspondant de la droite de régression y(x).

Pour calculer maintenant la variance de Y*(x), on l’écrit sous la forme:
```
Y*(x) = A (x-x^-) + Y^-
```
qui sera commode puisqu’on a vu que A et Y^- sont indépendantes. D’où la variance:
```
σ²[Y*(x)] = (x-x^-)² σ²(A)+ σ²(Y^-) = ((x-x^-)² / ∑_i=1ⁿ (x_i-x^-)² + 1/n) σ²
```
La quantité Y*(x)-y(x) / σ[Y*(x)] suit une loi normale réduite. Et en estimant σ par σ*, le quotient:
```
T= (Y*(x)-y(x))/σ*√[(x-x^-)²/∑_i=1ⁿ (x_i-x^-)² + 1/n]
```
suit une loi de Student-Fisher à (n-2) degrés de liberté. Cette propriété permet de trouver un intervalle de confiance pour y(x). Pour un risque α donné, on a:
```
yα(x) ∈ ax+b ± t_α/2 σ*√[(x-x^-)²/∑_i=1ⁿ (x_i-x^-)² + 1/n]
```
Lorsque x varie, les limites yα(x) décrivent une hyperbole. La droite de régression inconnue y(x) = αx + β se situe dans la zone comprise entre les deux branches de cette hyperbole.
Intervalle de confiance d'une observation

Un échantillon de n points a permis de déterminer les estimations a, b et σ*. Nous cherchons à faire des prévisions sur l’ordonnée y_n+1 d’un (n+1)ème point d’abcisse x_n+1 donnée. Cela revient à estimer y_n+1 et à déterminer son intervalle de confiance.

Pour estimer y_n+1 on prendra:
```
y*(x_n+1) = ax_n+1+b
```
qui est une estimation sans biais. En effet:
- y_n+1 est une réalisation de Y_n+1 = y(x_n+1) + ε_n+1 avec y(x_n+1) = αx_n+1 + β,
- y*(x_n+1) est une réalisation de Y*(x_n+1) = A x_n+1 + B
et, d’après 2.2, on a bien E [Y_n+1 - Y*(x_n+1)] = 0.

Pour déterminer maintenant la précision de cette estimation, il faut caractériser l’erreur de prévision (Y_n+1 - Y*(x_n+1)) en calculant sa variance. Ecrivons pour cela que:
```
Y_n+1-Y*(x_n+1) = (Y_n+1-y(x_n+1)) - (Y*(x_n+1)-y(x_n+1))
	= ε_n+1 - (Y*(x_n+1)-y(x_n+1))
```
Les deux quantités ε_n+1 et Y*(x_n+1) sont indépendantes puisque la seconde ne fait intervenir que les n premières observations, alors que la première concerne la (n+1)ème observation. Et, par conséquent, les variances s’ajoutent:
```
σ² [Y_n+1 - Y*(x_n+1)] = σ²(ε_n+1)+ σ² [Y*(x_n+1)] = σ² +((x_n+1-x^-)² ∑_i=1ⁿ (x_i-x^-)² + 1/n) σ²
```
Il en résulte que la variable centrée, réduite:
```
T= Y_n+1-Y*(x_n+1)/σ*√(1 + 1/n + (x_n+1-x^-)²/∑_i=1ⁿ (x_i-x^-)²)
```
suit une loi de Student à (n - 2) degrés de liberté, ce qui permet de trouver l’intervalle de confiance cherché.

On remarque, et c’est normal, que plus x_n+1 est éloigné de x^-, plus cet intervalle est grand. Il serait, de toute façon, illusoire et dangereux de prétendre faire des prévisions de Y(x) pour des valeurs de x qui se trouveraient en dehors de l’intervalle de variation des données expérimentales ayant permis de calculer les relations sur lesquelles reposent ces prévisions.

En fait, on simplifie le plus souvent l’expression de l’intervalle de confiance d’une observation en notant que, si x_n+1 n’est pas trop éloigné de x^-, la quantité (x_n+1 - x^-)² est généralement négligeable devant la quantité ∑_i=1ⁿ (x_i-x^-)², et en admettant que n est suffisamment grand pour que l’on puisse négliger 1/n devant 1.

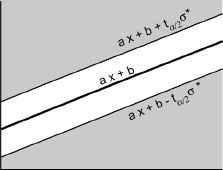
Dans ces conditions, la plage de confiance des observations, au risque α, est comprise entre les deux droites parallèles:
```
y=ax+b ± t_α/2 σ*
```

4 - Comparaison de deux régressions

Soit deux groupes d’individus, sur lesquels ont été mesurées les valeurs de deux variables Y et X: n₁ individus pour le premier groupe, et n₂ pour le second.

Im4

Désignons la droite des moindres carrés correspondant au premier groupe par:

y₁* = a₁x+b₁

et sa variance résiduelle estimée par σ₁*².

Désignons la droite des moindres carrés correspondant au second groupe par:

y₂* = a₂x+b₂

et sa variance résiduelle estimée par σ₂*².

La comparaison va porter successivement sur les variances, puis sur les pentes et, enfin, sur les ordonnées à l’origine. Les tests correspondants étant calqués sur ceux qui ont été mis en oeuvre pour la comparaison de deux populations, nous nous limiterons à leur principe.

Comparaison des variances

Le test à appliquer est celui de Snedecor, au quotient:

f = σ₁*²/σ₂*²

avec (n₁-2) degrés de liberté au numérateur, et (n₂-2) degrés de liberté au dénominateur.

Si l’hypothèse d’égalité des variances est acceptable (σ₁² = σ₂² = σ²), on peut adopter comme estimation de la variance commune la quantité:

σ*² = (n₁-2)σ₁*² + (n₂-2)σ₂*² / (n₁-2) + (n₂-2)

Comparaison des pentes

a₁ est une réalisation de la variable aléatoire A₁ de moyenne α₁ et de variance σ²/∑_i=1^n₁ (x_1i - x₁^-)².

a₂ est une réalisation de la variable aléatoire A₂ de moyenne α₂ et de variance σ²/∑_i=1^n₂ (x_2i - x₂^-)².

Sous l’hypothèse α₁ = α₂ = α la variable aléatoire (A₁ - A₂) suit une loi normale de moyenne nulle et de variance:

Im5

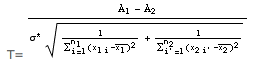
Donc la variable aléatoire:

Im6

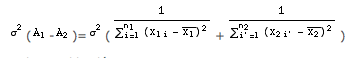
suit une loi de Student à (n₁ + n₂ -4) degrés de liberté, ce qui permet de tester l’égalité des pentes.

Comparaison des ordonnées à l'origine

La même démarche que ci-dessus permet d’établir que, sous l’hypothèse β₁ = β₂ = β, la variable aléatoire:

Im7

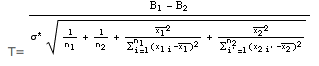
suit une loi de Student à (n₁ + n₂ - 4) degrés de liberté, ce qui permet de tester l’égalité des ordonnées à l’origine.

Exercices

Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !

Exercice 1

On a relevé pour chacune des années t de 1920 à 1938, numérotées de 1 à 19, la température moyenne x des mois d’été (en degrés centigrades) et la mortalité infantile y (nombre de décès d’enfants de moins d’un an pour 1000 naissances vivantes).

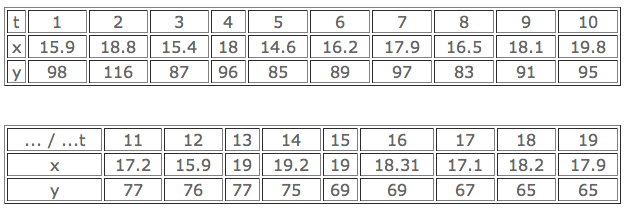
Après examen de ces chiffres et des graphiques auxquels ils peuvent donner lieu, indiquer les problèmes statistiques qu’ils vous paraissent poser et les calculs à faire pour les traiter.

Exercice 2

Le tableau ci-après donne les résultats d’un certain nombre de déterminations de la distance nécessaire (y en mètres) à l’arrêt par freinage d’une automobile lancée à différentes vitesses (x en km/h). Une étude graphique montre que la courbe représentant y en fonction de x est manifestement concave vers les y positifs, mais que si l’on utilise x² au lieu de x, la liaison apparaît sensiblement linéaire. Peut-on justifier ce fait par une loi physique ?

Admettant la validité de ce type de liaison entre y et x², on suppose de plus que la vitesse x peut être déterminée avec une grande précision et que les écarts constatés sont dûs à des fluctuations aléatoires de y autour d’une vraie valeur correspondant à une liaison linéaire représentée par l’équation y = αx 2 + β.

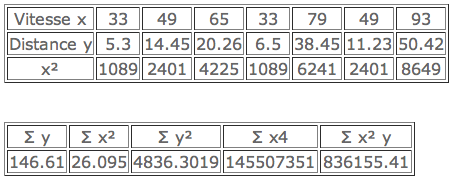
Quelle est la meilleure estimation de α et β ? Quelle hypothèse supplémentaire suppose cette estimation ?
Déterminer les limites de confiance à 95% pour les estimations de α et β.
Considérant le cas d’une voiture dont la vitesse est de 85 km/h, estimer la valeur moyenne correspondante de y. En donner une limite supérieure au seuil de confiance 99%.
On suppose que pour une voiture se déplaçant à 85 km/h, on observe une distance de freinage y = 55 mètres. Cette valeur peut-elle être considérée comme étant, à des fluctuations aléatoires admissibles près, d’accord avec l’équation d’estimation trouvée ?

Exercice 3

On a déterminé sur une série de 18 coulées Thomas la température y du bain d’acier liquide à la fin de l’opération (à l’aide d’un pyromètre à immersion) et la température x du centre de la flamme (à l’aide d’un pyromètre à flamme) juste avant le rabattement du convertisseur. Le tableau ci-dessous donne les résultats obtenus. Les températures sont exprimées en degrés centigrades.

Vérifier graphiquement que la régression de y en x peut être considérée comme linéaire.
Estimer l’équation de la droite de régression de y en x et l’écart-type de y lié par x. Avec quelle précision la température de la flamme permet-elle de connaître la température du bain d’acier dans les conditions des essais ?
Peut-on considérer que la différence entre y et x ne dépend pas de x ?

Exercice 4

Les données ci-dessous sont relatives à des mesures de la limite élastique y et de la résistance à la traction x en MPa d’alliages d’or destinés à des prothèses dentaires.

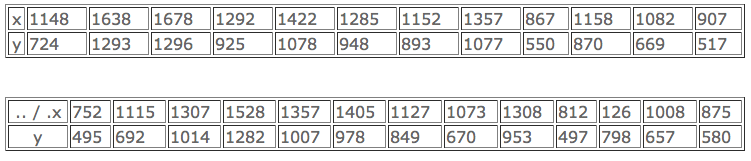
On donne les résultats de calculs suivants:

En admettant que E(Y/x) = αx + β, estimer α et β par la méthode des moindres carrés.
Calculer les intervalles de confiance à 95% de α et β.
Estimer la valeur moyenne de la limite élastique pour une résistance égale à 1290 MPa et calculer son intervalle de confiance à 90%.
Calculer l’intervalle de confiance à 90% pour la limite élastique correspondant à une résistance égale à 1290 MPa.

C'est un exercice classique de régression linéaire. La première question consiste à estimer les paramètres de la droite par la méthode des moindres carrés. Il est ensuite demandé de calculer leurs intervalles de confiance. Enfin, l'étudiant devra déterminer les intervalles de confiance d'un point de la droite et d'une observation.

Exercice 5

Les données ci-dessous sont relatives à l’étalonnage d’une méthode gravimétrique pour le dosage de la chaux en présence de magnésium. La variable en x est la teneur vraie et la variable en y est la teneur mesurée (en mg).

En admettant que E(Y/x) = αx + β, estimer α et β par la méthode des moindres carrés.
Caractériser la précision de la méthode gravimétrique.
Tester l’hypothèse α = 1 de telle façon que la probabilité d’accepter l’hypothèse si elle est vraie soit égale à 90%.
Tester l’hypothèse β = 0 de telle façon que la probabilité d’accepter l’hypothèse si elle est vraie soit égale à 90%.
Bâtir et mettre en oeuvre un test permettant de tester simultanément que α = 1 et que β = 0, la probabilité d’accepter l’hypothèse si elle est vraie étant encore égale à 90%.

A part la dertnière question, c'est un exercice classique de régression linéaire. La première question consiste à estimer les paramètres de la droite par la méthode des moindres carrés. Il est ensuite demandé de caractériser la précision de la méthode. Ensuite, l'étudiant doit mettre en place des tests classiques et conclure quant à la légitimité de la droite de régression. Enfin, il doit élaborer à la dernière question, un test qui teste simultanément les deux hypothèse testées précedemment.

Cet exercice propose les opérations habituelles d'étalonnage d'une méthode de mesure (quelle qu'elle soit) :

- peut-on considérer que la droite d'étalonnage a une pente égale à 1 ?

- peut-on considérer qu'elle passe par l'origine ?

- quelle est la précision de la mesure ?

a) Calculs préliminaires :

=31.1=31.01

∑=∑-n =427.9

∑=∑-n =438.889

∑(-)(-)=∑-n =430.49

Cela entraîne :

a= =1.00605

b=-a =- 0.2782

==0.9868

==(1-) =0.7242 ⇒ =0.8510

b) Précision de la nouvelle méthode. On cherche pour cela l'écart-type de e=Y(x)-(x).

[Graphics:HTMLFiles/index_146.gif]

Pour en déduire l'intervalle de confiance d'une observation qu'on pourrait faire. Cet écart-type vaut :

. Il dépend bien entendu de x.

Prenons une valeur de x, à une extrémité de l'intervalle qui a permis l'étalonnage de la méthode, par exemple : x=20 ou x=40 (c'est là que l'écart-type est maximal).

Cela donne :

0.8510 =0.96 (il est difficile de négliger les deux derniers termes sous la racine)

On peut donc dire que la précision est caractérisée par un écart-type inférieur à 0.96.

On peut aussi déterminer la taille maximale de l'intervalle de confiance pour une observation en faisant appel à une loi de Student-Fischer à 8 degrés de liberté :

± =± 2.306 × 0.96= ± 2.2

c) Testons l'hypothèse α=1 au risque 10%.

a est la réalisationd'une loi normale de moyenne α et d'écart-type σ/∑. On a donc :

=0.147, réalisation d'une loi de Student-Fischer à 8 degrés de liberté.

Or, la valeur lue dans la table de Student (8 degrés de liberté et risque de 10 %) vaut 1.86. Donc, l'hypothèse α=1 n'est pas infirmée avec 10 chances sur 100 de se tromper.

On peut donc admettre que la droite d'étalonnage a une pente égale à 1.

d) Testons l'hypothèse β=0 au risque 10%.

b est la réalisation d'une loi normale de moyenne β et d'écart-type σ. On a donc, dans le cadre de l'hypothèse faite :

(b - 0)/(σ^* (1/n + Overscript[x, _]^2/(∑ (x_i - Overscript[x, _])^2))^(1/2)) =- 0.213, réalisation d'une loi de Student à 8 degrés de liberté.

Cette valeur étant également inférieur à 1.86, on peut donc admettre que la droite d'étalonnage passe par l'origine.

e) Question difficile sans interprétation géométrique (on ne fait plus ça, c'était pourtant très pratique). Nous sommes donc ramenés aux décompositions suivantes :

=α +β+, mais puisqu'on teste α=1 et β=0, ça nous ramène à :

⇒ =, loi du à n degrés de liberté (par définition de ε)

Mais :

∑= ∑

= ∑

= ∑+∑+2∑(-)

= ∑+∑+2∑(a +b-)

= ∑+∑+2∑((a-1) +b )

= ∑+∑+2∑(a-1) +2∑b

= ∑+∑+2(a-1)∑ +2b∑

mais ∑=0 (polycopié chapitre 7, équation (1)) et ∑=0 (équation (2)). On arrive donc à:

∑= ∑+∑

Or :

, suit une loi du à 2 degrés de liberté

, suit une loi du à (n-2) degrés de liberté (voir polycopié)

Donc on peut construire :

f= qui obéit à une loi de Snédécor à (2,n-2) degrés de liberté.

On trouve : f=0.11 à comparer à 4.46. L'hypothèse passe donc largement.

[Graphics:HTMLFiles/index_205.gif]

Exercice 6

L’étude d’une méthode de dosage d’un élément dans des aciers a montré que, pour des échantillons de poids différents d’un même produit, les poids y de l’élément à doser variaient bien linéairement avec le poids x de l’échantillon, mais que la droite obtenue ne passait pas par l’origine.

Afin de vérifier l’hypothèse selon laquelle la solution acide utilisée en quantité fixe pour attaquer les échantillons contiendrait elle-même une certaine quantité de l’élément à doser, on s’est proposé de comparer les ordonnées à l’origine des droite de régression de y sur x obtenues pour deux aciers différents.

On a utilisé pour chacun des deux aciers 5 échantillons de poids équidistants, les mêmes pour les deux aciers soit 1, 2, 3, 4, 5. Les résultats obtenus sont les suivants:

Comparer les variances résiduelles
Peut-on considérer que les pentes sont statistiquement égales ?
Peut-on considérer que les ordonnées à l’origine sont statistiquement égales ?

Exercice 7

La figure suivante indique, pour les 21 régions françaises de province et de métropole, le PIB (y) par région en fonction du nombre d'emplois (x) dans la haute technologie, pour l'année 2000 (source: INSEE Nord-Pas-de-Calais). Le nuage de points, de forme allongée, suggère l'existence d'une relation linéaire (figurée par la droite des moindres carrées) entre ces deux variables.

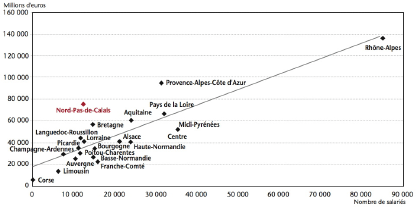
On donne par ailleurs les résultats intermédiaires suivants:

E10

Calculer les coefficients a et b, estimations des paramètres α et β de la relation linéaire (αx + β) qu'on cherche à mettre en évidence.
La relation obtenue est elle significative au risque 5% ?
Pour 12000 emplois de haute technologie, quelle est l'espérance mathématique du PIB et son intervalle de confiance à 95 % ?
Dans cette étude, la région Nord-Pas-de-Calais (cliente de l'étude) affiche un PIB de 76 Milliards d'euros pour environ 12000 emplois de haute technologie. Que pensez de cette région par rapport aux autres ?
La région Nord-Pas-de-Calais ainsi que la région Provence-Alpes-Côte d'Azur sont en effet assez éloignées du modèle obtenu. Selon vous, quelles raisons structurelles propres à ces régions pourraient expliquer cet écart ?

C'est encore un exercice classique de régression linéaire. La première question consiste à estimer les paramètres de la droite par la méthode des moindres carrés. Il est ensuite demandé de calculer leurs intervalles de confiance. Enfin, l'étudiant devra déterminer les intervalles de confiance d'un point de la droite et d'une observation et conclure sur les résultats

a) On peut dresser le tableau de calcul suivant :

Formulation	Calcul	Application numérique



		47267-1.40788×20533

	Résultat
	20533
	47267
	1.40788
	18359
	0.720615
	2.51749*10^^8
	15866.6

Les résultats trouvés concordent avec la droite dessinée sur le graphique.

b) On doit ici tester l'hypothèse α = 0.

a est la réalisation d'une loi normale de moyenne α et d'écart-type . Ainsi, sous l'hypothèse que α = 0, la quantité = = 7 est la réalisation d'une loi de Student à n-2=19 degrés de liberté.

Or 7 > 2.09 =. On peut donc rejeter l'hypothèse que α=0 avec moins de 5 chances sur 100 de se tromper et conclure que la relation est significative (elle l'est d'ailleurs à moins de 2 chances sur un million de se tromper).

c) L'estimation de l'espérance du PIB est donnée par l'équation de la droite des moindres carrés:

=1.40788×12000+18359= 35253 millions d'euros

L'intervalle de confiance recherché est celui d'un point de la droite. Il est donné par :

- <E(PIB) <+ .

=== 3864.32

=2.09.

d'où l'intervalle :

35253-2.09× 3864.32<E(PIB) <35253+2.09× 3864.32
27176.6<E(PIB)<43329.4

d) On recherche ici l'intervalle de confiance des observations (à 95%) donné par :

a x + b ± avec =2.09.

Ce qui donne :

35253 ±2.09

35253 ±34130 soit l'intervalle [1123, 69383]

Si on néglige les deux termes après le 1 dans la parenthèse sous la racine, on obtient :

35253 ±2.09

35253 ± 33161 soit [2092, 68414]

Ca ne change pas les conclusions mais l'approximation est un peu juste (on l'acceptera quand même).

En conclusion, avec moins de 5 chances sur 100 de se tromper, on peut dire que la région Nord-Pas-de-Calais a des caractéristiques différentes de celles des autres régions françaises sur le plan de l'impact des emplois de haute technologie sur le PIB.

e) L'article suggère les points suivants : Les régions Nord-Pas-de-Calais et Provence-Alpes-Côte d'Azur produisent en effet un PIB sensiblement supérieur à celui qu'elles devraient théoriquement dégager si le modèle linéaire décrivait la réalité. Avec 12000 emplois dédiés à la haute techologie, la région Nord-Pas-de-Calais devrait en théorie afficher un PIB beaucoup faible alors qu'il se situe à 76 milliards d'euros. Cela semble indiquer qu'il s'agit de régions qui tirent une partie importante de leur richesse, d'activités au caractère technologique moins prononcé. Effectivement, le Nord-Pas-de-Calais se caractérise depuis longtemps par la production d'une valeur ajoutée forte dans les industries de l'automobile, des biens intermédiaires et de l'agro-alimentaire. La région PACA, quant à elle, enregistre une valeur ajoutée conséquente dans le secteur tertiaire (activités immobilières, tourisme, administration, transports,...)

Ch.7 La Régression Linéaire

Introduction

La droite des moindres carrés

Propriétés statistiques de la droite des moindres carrés

La prévision statistique

Comparaison de deux régressions

Exercices

La Régression Linéaire

1 - La droite des moindres carrés

Nuage des individus

Caractérisation de la droite de régression

Analyse de la variance

Coefficient de corrélation

2 - Propriétés statistiques de la droite des moindres carrés

Le modèle de la régression linéaire

Propriétés de a et b

Estimation de s²

3 - La prévision statistique

Objectifs

Hypothèse de normalité

Test d'indépendance des variables

Test de nullité de l'ordonnée à l'origine

Intervalles de confiance pour une valeur donnée x de X

4 - Comparaison de deux régressions

Comparaison des variances

Comparaison des pentes

Comparaison des ordonnées à l'origine

Exercices

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7