Ch.6 Faits et modèles

PDF

Vidéo

Calculatrice

Statistiques > Ch.1: Probabilités et Variables Aléatoires Ch.2: La Loi Normale Ch.3: Le Contrôle Statistique Ch.4: L'Estimation Statistique Ch.5: Comparaisons Statistiques Ch.6: Faits et Modèles Ch.7: La Régression Linéaire Ch.8: L'Expérimentation Statistique

Faits et Modèles

Nous avons envisagé certaines lois de probabilité susceptibles de constituer des modèles pour les populations de références. Il s'agit maintenant, en présence d'observations, de choisir le modèle adapté et de vérifier que les observations disponibles s'y raccordent bien.

1 - Distributions statistiques

Mise en ordre des observations

Ayant effectué des observations sur les n individus constituant un échantillon, la mise en ordre consiste à grouper ensemble les résultats identiques, c’est-à-dire à faire correspondre, aux valeurs observées de la variable prise en considération, les nombres d’individus ayant présenté ces valeurs. Le tableau obtenu définit ce qu’on appelle une distribution statistique.

Dans le cas d’une variable susceptible de prendre les valeurs discrètes x₁,..., x_k,..., x_r, les résultats se présentent sous la forme du tableau ci-dessous.

Lorsque la variable est continue, il est commode de procéder à des groupages en classes. Cela consiste à diviser l’intervalle de variation de la variable en classes:

[x1-h/2 , x1+h/2[ , [x1+h/2 , x2+h/2[ ,..., [xr-1-h/2 , xr+h/2[

puis à grouper ensemble les valeurs observées qui tombent dans une même classe. Il est évident qu’une telle opération fait perdre de l’information; on peut montrer toutefois que la perte d’information est négligeable si l’on choisit l’intervalle de classe de façon à obtenir 10 à 15 classes.

Représentations graphiques des distributions

Nous allons décrire les trois représentations graphiques les plus utilisées, dans le cas d’une variable continue. La transposition au cas d’une variable discrète ne pose pas de problèmes.

1. Histogramme

   Ayant gradué l’axe des abcisses suivant les intervalles retenus, on construit sur chaque intervalle un rectangle de surface proportionnelle à la fréquence (absolue ou relative) des observations qui lui correspondent.

   

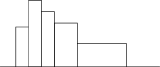
   La surface est préférée à la hauteur pour éliminer, quand les classes sont inégales, l’influence de cette inégalité.

2. Diagramme des fréquences cumulées

   C’est un graphe en escalier qui fait correspondre à chaque observation x, en abcisse, la fréquence, en ordonnée, des observations inférieures ou égales à x. On envisage le plus souvent les fréquences relatives, si bien que les fréquences cumulées sont comprises entre 0 et 1.

   

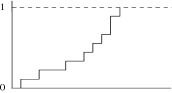
   Une autre façon, plus simple, de le construire est de définir des classes, de faire correspondre à chaque frontière supérieure la fréquence cumulée correspondante et de joindre les points par des segments de droite. Cela revient à admettre une distribution uniforme à l’intérieur de chacune des classes

   

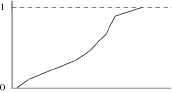
3. Boîte à moustaches

   Cette représentation a été imaginée récemment, dans le même courant d’idées que celui des statistiques robustes. Elle consiste en une " boîte " dont les côtés verticaux correspondent aux quartiles de la distribution et qui est traversée par un segment correspondant à la médiane.

   De part et d’autre de la boîte, on définit deux " moustaches " de longueur égale à 1,5 fois l’étendue interquartile. Si une observation dépasse une des moustaches, elle est considérée comme " aberrante " et individualisée. S’il n’y a pas d’observation aberrante, la moustache s’arrête à l’observation immédiatement supérieure (ou inférieure). Pour certains auteurs, les moustaches s'étendent jusqu'aux valeurs extrêmes même si celles-ci dépassent l'intervalle défini plus haut.

   

Caractéristiques des distributions

Rappelons que les caractéristiques essentielles sont:

• pour la tendance centrale, la moyenne m,
• pour la dispersion, la variance s².

Appelant f_k la fréquence relative n_k/n pour la valeur x_k (ou pour la classe de centre x_k), on peut écrire que m=∑f_k x_k et s² =∑f_k (x_k-m)².

S’il n’y a pas eu regroupement en classes, la fréquence de chaque valeur x_i est 1/n et on retrouve les formules habituelles m= 1/n ∑x_i et s² = 1/n ∑ (x_i-m)².

Il convient de noter la parenté évidente entre concepts statistiques et concepts probabilistes:

• à la notion de fréquence f_k, pour une distribution statistique, correspond celle de probabilité p_k, pour une loi de probabilité.
• à la notion de moyenne d’une distribution m=∑ f_k x_k correspond la notion d’espérance mathématique E(X) = ∑p_k x_k.
• enfin, à la notion de variance d’une distribution s² =∑ f_k(x_k-m)² correspond celle de variance d’une variable aléatoire σ² = ∑p_k (x_k-μ)².

2 - Fréquences et probabilités

Retour sur la loi des grands nombres

Considérons un ensemble de possibilités E et deux évènements complémentaires A et A^-. A est, par exemple, l’évènement: la variable X prend sa valeur dans un certain intervalle [x, x'[. Soit ϖ la probabilité de A; celle de A^- est donc égale à (1 - ϖ).

Faisons successivement n épreuves (expériences) identiques, et supposons qu’au cours de ces n épreuves, A se produise k fois et A^-, par conséquent, (n - k) fois. La fréquence relative de A est f_n=k/n. L’expérience montre que, si n est assez grand, f_n est voisin de ϖ. C’est la fameuse loi des grands nombres due à Bernouilli en 1713, et qui jette un pont entre fréquences et probabilités

Nous avons démontré, au chapitre 4 en partant de l’inégalité de Bienaymé-Tchebichef, qu’étant donnée une suite de variables aléatoires indépendantes et suivant la même loi de probabilité, leur moyenne convergeait en probabilité vers la moyenne de la loi. Appliquée à la moyenne de n variables de Bernouilli X₁,..., X_n, cela va permettre de démontrer ce qui précède.

En effet, soit F_n = (X₁ +... + X_n)/n cette moyenne. Elle a pour espérance ϖ et pour variance ϖ(1-ϖ)/n et l’inégalité de Bienaymé-Tchebichef pemet d’écrire que:

Prob{|Fn-ϖ| > ε} ≤  ϖ(1-ϖ)/(nε²)

Ce résultat s’énonce ainsi: ε étant un nombre positif arbitraire, aussi petit que l’on veut, la probabilité pour que la fréquence relative F_n s’écarte de la probabilité ϖ d’une quantité supérieure à ε, tend vers 0 lorsque le nombre d’épreuves augmente indéfiniment.

D’un point de vue pratique, cela exprime qu’en faisant un nombre suffisant d’épreuves, il est possible d’avoir une "idée" aussi précise qu’on le veut de la probabilité ϖ qu’on ne connaît pas. Il suffit, par exemple, de faire un nombre assez grand de tirages dans une urne de composition inconnue (proportion ϖ de boules noires) pour que la fréquence observée des boules noires soit presque sûrement très voisine de la proportion ϖ. La loi des grands nombres constitue, à ce titre, la base de la statistique mathématique.

Nombre de mesures à effectuer pour une précision donnée

L’inégalité de Bienaymé-Tchebichef majore beaucoup la probabilité cherchée. Il en résulte que la valeur de n qu’il faut dépasser pour que cette probabilité n’excède pas un seuil fixé, est inutilement grande. Souhaitant, par exemple, estimer une proportion (ou une probabilité) ϖ voisine de 0.2 avec une précision égale à ± 0.01 et un risque de 5%, l’application de l’inégalité de Bienaymé-Tchebichef conduit à un nombre n très grand puisque:

0.05 = Prob{|Fn-ϖ| > 0.01} ≤ (0.2x0.8)/(n(0.01)²) ⇒ n≥32000

Il est préférable d’utiliser le théorème central limite qui établit que, si n est suffisamment grand, la fréquence relative obéit à une loi qui s’approche d’une loi normale de moyenne ϖ et de variance ϖ(1-ϖ)/n. D’où il résulte que la variable aléatoire

Un = (Fn-ϖ)/√(ϖ(1-ϖ)/n) suit approximativement une loi normale réduite

Il s’ensuit que:

Prob{|Fn-ϖ| > ε} = 2 Prob{U > ϵ/√(ϖ(1-ϖ)/n) }

qui conduit, avec les mêmes données que ci-dessus, à:

0.05 = 2 Prob{U > 0.01/√(0.2x0.8/n}

et, après lecture dans la table de la loi normale réduite, à n ≥ 984.

On peut constater que c’est généralement l’ordre de grandeur de la taille des échantillons constitués pour les sondages d’opinion.

Estimation d'une proportion et intervalle de confiance

Puisque E(F_n) = ϖ et que σ²(F_n) = ϖ(1-ϖ)/n →0, F_n est un estimateur sans biais de ϖ.

D’autre part, l’approximation de la loi de F_n par une loi normale permet d’écrire, au risque α près, que:

|fn-ϖ|≤ uα/2 √(ϖ(1-ϖ)/n), où uα/2 est lu dans une table de la loi normale réduite

Si n est suffisamment grand, on peut approximer le deuxième membre de l’inégalité en remplaçant ϖ par son estimation f_n. D’où l’intervalle de confiance, au risque α:

fn - uα/2 √(fn(1-fn)/n) < ϖ < fn + uα/2 √(fn(1-fn)/n)

Comparaison de deux proportions

Soit ϖ₁ et ϖ₂ les proportions caractérisant deux populations, et soit f₁ et f₂ les fréquences observées sur deux échantillons, de tailles respectives n₁ et n₂, prélevés au hasard dans chacune de ces populations. Faisant l’hypothèse que ϖ₁ = ϖ₂ =ϖ, une démarche calquée sur celle mise en oeuvre pour la comparaison de deux moyennes, permet d’établir que, en estimant ϖ par la quantité ϖ* = (n₁f₁+n₂f₂)/(n₁+n₂), le quotient:

u = (f1-f2)/√(ϖ*(1-ϖ*)(1/n1 + 1/n2))

est approximativement une réalisation d’une variable normale réduite, si l’hypothèse est vraie. Il suffit, pour tester l’hypothèse, de placer u par rapport à l’intervalle correspondant au risque choisi.

Métrique du χ²

Soit p(x) la densité de probabilité d’une variable aléatoire X. La probabilité pour que X prenne une valeur dans l’intervalle [x_k-h/2 , x_k+h/2[ est égale à ϖ_k = ∫_xk-h/2^x_k+h/2 p(x)dx, et la probabilité pour que X prenne une valeur en dehors de cet intervalle est (1- ϖ_k). Pour un échantillon de n observations de la variable X, le nombre de valeurs n_k tombant dans l’intervalle [x_k-h/2 , x_k+h/2[ est une réalisation d'une variable N_k qui suit une loi binomiale de moyenne n ϖ_k et de variance n ϖ_k (1 - ϖ_k), et lorsque n augmente N_k converge en probabilité vers n ϖ_k.

Pour tenir compte de toutes les classes, soit n₁,..., n_k,..., n_r les effectifs observés dans les classes et soit ϖ₁,..., ϖ_k,..., ϖ_r, les probabilités théoriques correspondant à la loi de référence. On définit ce qu’on appelle les effectifs théoriques dans les classes, qui sont les quantités n ϖ₁,..., n ϖ_k,..., n ϖ_r. Notons qu’effectifs observés et théoriques ont même somme n.

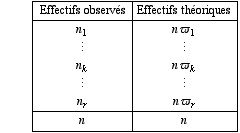
Pour mesurer la distance entre distribution observée des n_k et distribution théorique des nϖ_k, on peut envisager plusieurs quantités.

L’une d’elle est la distance de Kolmogorov qui est la quantité:

D=sup{ |nk-nϖk| }

Mais on retient le plus souvent ce qu’on appelle la distance du χ² qui est la quantité:

χ² = ∑k=1r (nk-nϖk)²/(nϖk)

Nous allons montrer que, si l’échantillon provient bien d’une population définie par la loi de probabilité envisagée, cette quantité est une réalisation d’une loi du χ² à (r-1) degrés de liberté: nombre de classes moins 1.

La démonstration qui suit n’est pas essentielle. Pour simplifier les notations, nous la ferons dans le cas de trois classes, mais elle est facilement transposable au cas général.

Soit les variables: X₁ = N₁-nϖ₁/√(nϖ₁), X₂ = N₂-nϖ₂/√(nϖ₂), X₃ = N₃-nϖ₃/√(nϖ₃).

La variable dont nous cherchons la loi est χ² = X₁² + X₂² + X₃². Les variables X₁, X₂, X₃ suivent à la limite, quand n augmente, des lois normales centrées et de variances respectives: (1-ϖ₁), (1-ϖ₂), (1-ϖ₃), mais elles ne sont pas indépendantes puisque: N₁ + N₂ + N₃ = n et, par conséquent: √ϖ₁ X₁ + √ϖ₂ X₂ + √ϖ₃ X₃ =0.

Calculons les covariances E(X₁ X₂), E(X₂ X₃), E(X₃ X₁). Pour cela, multiplions l’égalité précédente par X₁, puis X₂, puis X₃. On obtient:

√ϖ1 E(X1²)+ √ϖ2 E(X1 X2)+ √ϖ3 E(X1 X3) =0

√ϖ1 E(X1 X2)+ √ϖ2 E(X2²)+ √ϖ3 E(X2 X3) =0

√ϖ1 E(X1 X3)+ √ϖ2 E(X2 X3)+ √ϖ3 E(X3²) =0

Tenant compte de ce que: E(X₁²) = (1- ϖ₁), E(X₂²) = (1- ϖ₂), E(X₃²) = (1- ϖ₃), et de ce que: ϖ₁ + ϖ₂ + ϖ₃ = 1, on trouve, après résolution du système linéaire:

E(X1 X2) = -√(ϖ1ϖ2)

E(X2 X3) = -√(ϖ2ϖ3)

E(X1 X3) = -√(ϖ1ϖ3)

Cela étant, le vecteur OP^⇀ (X₁, X₂, X₃) est orthogonal au vecteur unitaire u^⇀ (√ϖ₁, √ϖ₂, √ϖ₂).

Faisons un changement de coordonnées orthonormales en prenant l’un des axes passant par le vecteur u^⇀. Les nouvelles coordonnées de OP^⇀ seront:

Y1 = a1 X1 + a2 X2 + a3 X3

Y2 = b1 X1 + b2 X2 + b3 X3

Y3 = ϖ1 X1 + ϖ2 X2 + ϖ3 X3

Et, dans ce nouveau système, χ² = Y₁² + Y₂².

Les six valeurs des coefficients a et b sont déterminées d’une infinité de façons par les cinq relations:

a1² + a2² + a3² = 1

b1² + b2² + b3² =1

a1 b1 + a2 b2 + a3 b3 =0

√ϖ1 a1 + √ϖ2 a2 + √ϖ3 a3 =0

√ϖ1 b1 + √ϖ2 b2 + √ϖ3 b3 =0

Chacune des variables Y suit une loi normale puisque toute fonction linéaire de variables normales suit une loi normale. Calculons leurs variances E(Y₁²), E(Y₂²) et leur covariance E(Y₁ Y₂). On a, pour une fonction linéaire:

E(Y1²) = a1² (1- ϖ1)+ a2² (1- ϖ2)+ a3² (1- ϖ3)-2(a1 a2 √(ϖ1 ϖ2) + a1 a2 √(ϖ2 ϖ3) + a1 a3 √(ϖ1 ϖ3))

E(Y1²) = a1² + a2² + a3² - (a1 √ϖ1 + a2 √ϖ2 + a3 √ϖ3)²

E(Y1²) = 1

On peut montrer, de la même façon, que E(Y₂²) = 1 et que E(Y₁ Y₂) = 0. Par suite Y₁ et Y₂ sont des variables normales centrées, réduites et indépendantes, la condition E(Y₁ Y₂) = 0 étant nécessaire et suffisante pour l’indépendance de variables normales.

Donc la variable χ² = Y₁² + Y₂² est la somme des carrés de deux variables normales, réduites, indépendantes et suit, par conséquent, une loi du χ² à deux degrés de liberté: nombre de classes moins un.

3 - Techniques de raccordement entre distributions statistiques et lois de probabilité

Loi de référence

Le problème, sous la forme la plus générale, consiste à caractériser à partir des données le type de la loi de référence, puis à préciser cette loi par estimation des paramètres qui la définissent complètement. En pratique, cependant, on n’opère pas exactement ainsi. Les lois de référence s’identifiant le plus souvent aux lois de probabilité fondamentales (loi binomiale, normale, log-normale), il s’avère plus simple:

• de rapprocher la distribution examinée de la loi de probabilité à laquelle il semble intuitivement (ou pour des raisons théoriques) qu’elle doive se raccorder;
• de vérifier ensuite la validité du rapprochement ainsi opéré.

Lorsque le raccordement à l’une des lois fondamentales s’avère injustifié, il y a lieu de faire appel à d’autres lois de référence, et il en existe un nombre considérable (loi gamma, loi beta, loi de Pareto, loi de Gumbel, loi de Weibull,...), ou d’en créer éventuellement pour la circonstance.

Détermination du type de la loi de référence

Il n’y a pas de recette particulière à mettre en jeu pour déterminer le type de la loi de référence à laquelle on soupçonne la distribution observée de se rattacher. En général, on se laisse guider par des considérations logiques ou bien, plus simplement, on tente des rapprochements qui semblent résulter de la forme même des distributions observées. Dans le cas de distributions relatives à des variables discrètes, le raccordement à des lois de référence binomiale ou de Poisson s’impose de prime abord.

Dans le cas de variables continues, le raccordement à des lois de référence normale ou log-normale s’avère très souvent, mais pas toujours, légitime. En vue de vérifier, avant tout calcul compliqué, que l’hypothèse de tels raccordements n’est pas a priori absurde, on dispose d’ailleurs de moyens simples et rapides.

1. Raccordement à une loi normale

   La loi normale est une loi symétrique. De plus, on a vu que l’intervalle [μ ± u σ [comprend approximativement la probabilité: 50% pour u = 2/3, 68% pour u = 1, 95% pour u = 2 et presque 100% pour u = 3. Si donc une distribution observée en pratique est telle que les fréquences des observations comprises à l’intérieur de ces intervalles sont voisines de ces probabilités, il y a présomption de normalité.

   On peut également vérifier cette présomption à l’aide d’une transformation connue sous l’ap-pellation de droite de Henry. Soit P(x) le graphe de la fonction de répartition d’une loi normale; il a une forme en S. Il existe dans le commerce un papier dit "gausso-arithmétique" qui, par un changement d’échelle de l’axe des ordonnées, permet de réaliser une anamorphose de P(x) qui le transforme en une droite. Dès lors, si l’on trace sur ce papier le diagramme des fréquences cumulées de la distribution observée et que ses points sont sensiblement alignés, on peut penser que le raccordement à une loi normale est légitime. Un tel graphique est réalisé par tous les logiciels de calculs statistiques.

2. Raccordement à une loi log-normale

   Pour reconnaitre sommairement si une distribution observée est du type log-normal, il est également commode d’utiliser un graphique de Henry avec échelle des abcisses logarithmique (papier gausso-logarithmique). On procède alors à la détermination du paramètre θ₀ par tâtonnement ou, ce qui est mieux, par remarques d’ordre technique.

Estimation des paramètres de la loi de référence

La loi de référence dépend le plus souvent d’un certain nombre de paramètres qu’il est nécessaire d’estimer pour la définir complètement. Une loi binomiale ou de Poisson est entièrement définie par la proportion ϖ à laquelle elle correspond (n étant connu). Une loi normale est entièrement définie par sa moyenne μ et son écart-type σ. Il convient donc, à partir des données disponibles, d’estimer soit la proportion ϖ, soit la moyenne μ et l’écart-type σ de la loi de référence binomiale, de Poisson ou normale, pour ne considérer que ces trois lois là.

Vérification de la légitimité d'un raccordement effectué

La comparaison des n_k observés et des n ϖ_k théoriques met en évidence des différences plus ou moins fortes. Cela n’a rien d’étonnant puisque, dans l’hypothèse où le raccordement opéré est justifié, la distribution des n ϖ_k n’est que la loi limite de la distribution des n_k. Il reste toutefois à savoir si les différences ainsi mises en évidence sont compatibles avec les seuls aléas de l’échantillonnage. Ce n’est en effet qu’à cette condition qu’on peut considérer le raccordement opéré comme légitime.

La vérification consiste à déterminer la loi d’une certaine fonction de l’ensemble des fluctuations entre effectifs observés et théoriques, dans l’hypothèse où ces fluctuations ne sont effectivement dues qu’aux aléas de l’échantillonnage.

Retenant la fonction χ² = ∑_k=1^r (n_k-nϖ_k)²/nϖ_k, nous avons montré que, dans ces conditions, elle était une réalisation d’une loi du χ². A un seuil de probabilité α faible pouvant être considéré comme négligeable correspond une valeur χ_α² telle que la probabilité d’observer χ² > χ_α² soit justement égale à α.

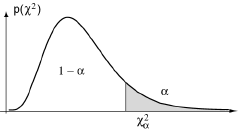
Si la valeur χ² observée est supérieure à χ_α², il parait préférable de mettre en doute l’hypothèse de la légitimité du raccordement. Si, au contraire, χ² est inférieur à χ_α², il n'y a pas de raison de mettre en doute cette hypothèse. Comme on s'y est déjà habitué, cela ne signifie malheureusement pas qu'elle soit vraie. Or ce que l'on souhaiterait généralement c'est confirmer la validité du modèle envisagé. L'aspect négatif du test statistique, dans le sens où il ne prend pas en compte le risque de conserver à tort l'hypothèse faire, est gênant dans ce cas précis.

Notez que l'on a effectué un test à droite, puisque ce sont des écarts importants entre effectifs observés et théoriques que l'on veut éventuellement détecter, donc une valeur grande du χ². Ajoutons enfin deux remarques sur la mise en oeuvre du test.

La première est que, pour que la loi de la quantité χ² soit suffisamment voisine d’une loi du χ², il faut non seulement que n soit assez grand, mais encore que les nombres n ϖ_k ne soient pas trop petits: en pratique ils ne doivent pas être inférieurs à 5. Si certains d’entre eux sont trop petits, il est nécessaire de procéder à des groupages de classes.

La seconde remarque est que, le plus souvent, la loi de référence dépend d’un ou plusieurs paramètres inconnus. A ce moment là, les n ϖ_k sont calculés non pas à partir des paramètres véritables de la loi, mais à partir des paramètres estimés. Ils sont donc eux-mêmes aléatoires. On démontre alors que le nombre de degrés de liberté de la loi du χ² à laquelle il faut se référer est égal à (r-1-p), où p est le nombre de paramètres estimés.

4 - Tests non paramétriques

Fort souvent on est amené à prendre en considération des variables dont on ignore la distribution. Il n’est alors plus possible de se référer aux tests de comparaison décrits dans le chapitre 5. Pour lever cette difficulté, on s’est donc préoccupé de définir des tests, dits non paramétriques, ne faisant aucune hypothèse sur la nature des populations mises en jeu.

Il existe une très grande variété de tels tests non paramétriques, mais nous nous limiterons à la présentation de ceux qui sont les plus utilisés et qui se trouvent reposer sur la prise en compte d’une même quantité χ² que le test ci-dessus du raccordement entre une distribution observée et une distribution théorique.

Test de comparaison de plusieurs populations qualitatives

Soit p populations P₁,..., P_i,..., P_p dont les individus sont distingués suivant r catégories C₁,..., C_k,..., C_r qui peuvent être les modalités d’une variable qualitative (ou les classes d’une variable quantitative). Pour deux lots de pièces, par exemple, classées en bonnes ou mauvaises, on a p = 2 et r = 2.

On a prélevé un échantillon dans chacune de ces populations. Soient n₁,..., n_j,..., n_p, leurs tailles et soit n_jk le nombre d’individus qui proviennent de la population P_j et qui appartiennent à la catégorie C_k.

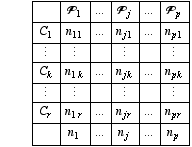
Si l’on fait l’hypothèse que les populations sont identiques, alors les probabilités d’appartenir à chacune des classes sont les mêmes pour toutes les populations, soit ϖ₁,..., ϖ_k,..., ϖ_r, et l’on peut définir des effectifs théoriques dans chaque classe et pour chaque population: n_j ϖ_k pour la classe C_k de la population P_j. Il semble naturel d’estimer la probabilité dans la classe C_k par:

ϖk* = ∑j=1p njk / ∑j=1p nj

et d’envisager la quantité:

χ² = ∑j=1p ∑k=1r (njk - njϖk*)² / (njϖk*)

pour tester l’hypothèse d’identité des populations. On montre que, sous cette hypothèse, elle obéit à une loi du χ² à (p(r-1) - (r-1)) = (p-1)(r-1) degrés de liberté.

Test de la médiane

Etant donnés les résultats fournis par deux échantillons de taille n₁ et n₂:

échantillon 1: x1, x2,..., xn1

échantillon 2: y1, y2,..., yn2

Arrangeons l’ensemble de ces résultats selon une même suite croissante: x₁, y₁, y₂, x₂, y₃, x₃,... et désignons la médiane de cette suite par M.

Après décompte des observations au dessus et en dessous de M, le tableau des données peut être résumé ainsi.

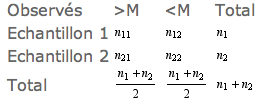
Dans l’hypothèse où les deux populations sont identiques, la proportion théorique des observations au dessus et en dessous de la médiane est dans tous les cas 1/2. Au tableau précédent correspond le tableau théorique ci-contre, et on est en définitive ramené à un test du χ² avec un degré de liberté.

Test des signes

Ce test s’applique à des observations appariées. Sur un même individu i on a effectué deux mesures y_i et x_i et on s’intéresse aux différences d_i = y_i-x_i. Dans le test classique on prenait en compte les valeurs de ces différences, mais dans le test des signes on ne retiendra que les signes, plus ou moins, de ces différences. Il y a donc perte d’information.

S’il n’y a pas de différence entre les mesures, la probabilité d’un signe plus est égale à celle d’un signe moins et égale à 0.5. S’il y a n individus dans l’échantillon, les effectifs théoriques sont égaux à 0.5 n et on est encore ramené à un test du χ² avec un degré de liberté sur la quantité:

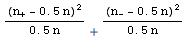
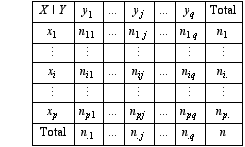
Test d'indépendance entre deux variables qualitatives

Soit x₁,..., x_i,..., x p et soit y₁,..., y_j,..., y q les modalités de deux variables qualitatives X et Y. Un échantillon de n individus sur lesquels ont été repérées les valeurs prises simultanément par les deux variables a donné les résultats ci-contre: n ij est le nombre d’individus ayant présenté à la fois la valeur x_i de X et la valeur y_j de Y. n_i. et n_.j représentent respectivement le total de la ligne x_i et celui de la colonne y_j.

Soit les probabilités suivantes:

ϖi. = Prob{X=xi}

ϖ.j = Prob{Y=yi}

ϖij = Prob{X=xi et Y=yj}

Faisons l’hypothèse que les deux variables sont indépendantes. Il s’ensuit, d’après le théorème des probabilités composées, que:

ϖij = ϖi. ϖ.j

Estimons ϖ_i. et ϖ_.j respectivement par ϖ_i.* = n_i./n et ϖ_.j* = n_.j/n, donc ϖ_ij par ϖ_ij* = n_i.n_.j/n².

Sous l’hypothèse d’indépendance, l’effectif théorique correspondant à l’effectif observé n_ij est égal à n ϖ_ij* = n_i.n_.j/n et la quantité:

∑i=1p ∑j=1q [(nij - ni.n.j/n)2] / [ni.n.j/n]

obéit à une loi du χ² à (p-1)(q-1) degrés de liberté.

Exercices

Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !

Exercice 1

Il y a dans un certain pays 25% d’illettrés. On considère les 400 prisonniers d’une prison de ce pays.

1. Calculer, en admettant que l’échantillon constitué par les prisonniers est tiré au hasard dans la population du pays, la probabilité pour que la fréquence des prisonniers illettrés dépasse 35% ?
2. Quelle valeur cette fréquence n’a-t-elle qu’une chance sur 100 de dépasser ?

Exercice 2

Un sondage d’opinion sur les intentions de vote d’un certain électorat a porté sur un échantillon de 2500 électeurs représentatifs de cet électorat et a fourni les résultats suivants: 1200 électeurs favorables au candidat A et 1300 favorables au candidat B.

1. En admettant que la proportion ϖ inconnue de l’électorat favorable au candidat B soit égale à 0.5 (ballotage), donner la fourchette dans laquelle la fréquence relative à un échantillon de 2500 électeurs aurait la probabilité 95% de tomber.
2. Que penser d’un journal qui annoncerait, au vu des résultats du sondage, l’élection du candidat B ?
3. Quelle devrait être la taille de l’échantillon pour qu’une différence de 4% entre les fréquences (48% favorables à A et 52% à B) permette de conclure, avec moins de une chance sur 100 de se tromper, à l’élection du candidat B ?

Exercice 3

Une enquête réalisée auprès de 4000 foyers d’une grande ville en 1990 a montré que 1944 d’entre eux possédaient une machine à laver la vaisselle. Une enquête réalisée dans la même ville en 1995 sur 5000 foyers a montré que 2587 possédaient un tel appareil. Peut-on admettre que le taux d’équipement a augmenté ?

Exercice 4

La direction du marketing d’une entreprise a fait procéder à une enquète auprès d’un échantillon de n consommateurs en leur soumettant deux modes de présentation A et B d’une même marchandise et en leur demandant de faire connaître leur préférence. Soient n 1 et n 2 les nombres de consommateurs ayant préféré respectivement les présentations A et B et soient ϖ₁ et ϖ₂ les proportions correspondantes dans la population. n 1 et n 2 sont des réalisations de variables aléatoires liées par la relation N₁ + N₂ = n. On est amené à se demander si la différence constatée d = n 1 - n 2 est significative d’une préférence réelle dans la population pour l’un des modes de présentation.

1. d est une réalisation d’une variable D que l’on peut écrire D = 2 N₁ - n. Calculer sa moyenne et sa variance.
2. On se propose de tester l’hypothèse d’une différence nulle ϖ₁ - ϖ₂ = 0, dans la population échantillonnée. Quelle est l’estimation de la variance de D qui vous parait devoir être utilisée ? A quelle condidion doit satisfaire la différence d pour qu’elle puisse être considérée comme significative au niveau de signification 95% ?

Exercice 5

Sur un échantillon de 10000 bébés, 5136 sont des garçons et 4864 sont des filles. Peut-on admettre que les probabilités pour qu’un bébé soit un garçon ou une fille sont égales ?

Exercice 6

On effectue des croisements de poules blanches et noires. D’après les lois de Mendel, lorsqu’on effectue un tel croisement, on a 1 chance sur 4 d’obtenir une poule blanche, 1 chance sur 4 d’obtenir une poule noire et 1 chance sur² d’obtenir une poule bleue (hybride). Les 158 croisements effectués ont donné 43 poules blanches, 40 poules noires et 75 poules bleues. Ces résultats vous paraissent-ils compatibles avec les lois de Mendel ?

Cet exercice simple permet à l'étudiant d'apprendre à mettre en oeucvre la métrique du khi2 afin de tester la ligitimité d'un raccordement à une loi.

	observés	théoriques
Blanches	43	39.5	0.310
Noires	40	39.5	0.006
Bleues	75	79	0.203
∑	158	158	0.519

Il n'est même pas besoin de regarder la table du . La valeur trouvée est inférieure à l'espérance d'un à 2 degrés de liberté qui est égale à 2.

On conclut donc que les résultats sont compatibles avec les lois de Mendel. Néanmoins, la distance est tellement petite qu'on peut présumer une triche sur les données.

Exercice 7

On considère ci-dessous la distribution du dernier chiffre de 200 lectures de pesée. Peut-on craindre que celui qui effectuait les pesées a une préférence pour certains chiffres ? Peut-on justifier cette crainte ?

Cet exercice classique permet à l'étudiant de tester la ligitimité d'un raccordement à une loi et de conclure quant au caractére aléatoire des résultats énoncés.

x	0	1	2	3	4	5	6	7	8	9	∑
obs	35	16	15	17	17	19	11	16	30	24	200
th	20	20	20	20	20	20	20	20	20	20	200
	11.25	0.8	1.25	0.45	0.45	0.05	4.05	0.80	5.00	0.80	24.90

Le (5%) pour 9 degrés de liberté est égal à 16.9.

Pour 5‰, il est égal à 23.6. La valeur calculée lui est supérieure : il y a donc moins de 5 chances sur 1000 que la répartition soit au hasard : préférence pour 0, 8 et non préférence pour6.

Exercice 8

La direction du personnel d’une usine veut déterminer si le nombre d’avis d’arrêt pour maladie dépend du jour de la semaine. Pendant la période étudiée, il y a eu 720 avis d’arrêt. Les cas de maladie du samedi après-midi où l’on ne travaille pas ne sont notifiés que le lundi. Chaque jour on notifie les arrêts survenus entre la veille 17 h et le jour 17 h, sauf le samedi où l’on s’arrête à 13 h et le lundi où sont notifiés les arrêts du samedi 13 h au lundi 17 h. Faisant l'hypothèse d'une répartition uniforme des arrêts, que peut-on conclure de cette enquête ?

L'exercice se résout comme le précédent : l'étudiant est améné à tester la ligitimité d'un raccordement à une loi et àconclure quant au caractére aléatoire des résultats énoncés.

Pour calculer les effectifs théoriques, on se rapportera au volume horaire correspond à chacune des journées :

	heures	th	obs
Lundi	4+24+24=52		189	4.91
Mardi	24		100	0.09
Mercredi	24	103	127	5.59
Jeudi	24	103	115	1.40
Vendredi	24	103	102	0.01
Samedi	20		87	0.01
	∑	720	720	12.01

Pour 5 degrés de liberté, le (5%) est égale à 11.1.

On a donc moins de 5 chance sur 100 d'être "injuste" si l'on soupçonne les gens de tomber plutôt malade en milieu de semaine que pendant le week-end.

Exercice 9

La fabrication de pièces dans un atelier de mécanique donne lieu à un certain pourcentage de pièces rebutées comme non utilisables. On a observé 100 lots différents de 100 pièces chacun qui ont donné les résultats suivants.

1. Quelle distribution théorique paraît devoir donner une bonne description de la distribution observée et pour quelle raison ?
2. Tester l’accord entre les observations et le modèle.

L'exercice se résout toujours comme le précédent à la différence près que l'étudiant est amené à choisir la distribution thèorique et ensuite à tester l'accord entre ce modèle et les observations.

La moyenne du nombre de rebuts est égale à =5. La distribution étant discrête, on songe à la loi binomiale ou la loi de Poisson. Mais n=100 grand et ϖ=5% faible, on préfère donc la loi de Poisson, de paramètre λ=5. Ce qui permet de remplir le tableau ci dessous :

	0	1	2	3	4	5	6	7	8	9	10	≥11	∑
obs	0	2	9	14	20	18	15	9	6	4	2	1	100
th	0.67	3.37	8.43	14.03	17.55	17.55	14.62	10.44	6.53	3.63	1.81	1.37	100

Compte tenu de classes d'effectif théorique inférieur à 5, il convient de faire des regroupements (notez également que la dernière classe était "≥ 11"):

	≤2	3	4	5	6	7	8	≥9	∑
obs	11	14	20	18	15	9	6	7	100
th	12.47	14.03	17.55	17.55	14.62	10.44	6.53	6.81	100
	0.17	0.00	0.34	0.01	0.01	0.20	0.04	0.01	0.78

Il y a 6 degrés de liberté (8 classses, total = 100 et λ estimé). La valeur du correspondant à 1% à gauche est égale à 0.872. Il y a donc moins de 1 chance sur 100 d'observer un raccordement aussi bon.

Exercice 10

On a mesuré les duretés Rockwell sur 100 tôles minces en faisant 3 mesures au centre, dont on a pris la moyenne. Les résultats des mesures, une fois ordonnés et mis en classes, ont été rassemblés dans le tableau suivant.

Que penser du raccordement à une loi normale ? Tracer la droite de Henry.

Cet exercice permet de tester graphiquement le raccordement des observations à une loi normale en utilisant du papier gausso-arithmétique puis de tester ce raccordement à l'aide de la loi du khi2.

Pour dessiner la droite de Henry, il nous faut les fréquences cumulées :

	53.5	54.5	55.5	56.5	57.5	58.5	59.5	60.5	61.5	62.5	63.5	64.5	∑
	1	4	8	13	16	19	14	11	6	5	2	1	100
	1	5	13	26	42	61	75	86	92	97	99	100	%

Le raccordement par la droite de Henry est très correct : ne pas tenir compte des observations extrêmes toujours très dispersées.

En profiter pour estimer la moyenne qui, pour une loi normale est aussi la médiane (fréquence cumulée égale à 50%) ; ainsi que l'écart-type puisque dans l'intervalle de probabilité compris entre 2.5% et 97.5% il y a 2×1.96 fois l'écart-type (==2.3)

On pourra aussi estimer moyenne et écart-type par le calcul à partir de :

=m= ==58.03

= -=3372.55-3367.48=4.07 ⇒ =s=2.03

Puis éventuellement (mais ça n'est pas demandé) tester le raccordement avec la loi du :

	53.5	54.5	55.5	56.5	57.5	58.5	59.5	60.5	61.5	62.5	63.5	64.5	∑
obs	1	4	8	13	16	19	14	11	6	5	2	1	100
th	1.28	2.82	6.53	11.92	17.15	19.45	17.40	12.26	6.82	2.99	1.03	0.07	100

Pour lequel il faut regrouper des classes :

	≤55.5	56.5	57.5	58.5	59.5	60.5	≥61.5	∑
obs	13	13	16	19	14	11	14	100
th	10.63	11.92	17.15	19.45	17.40	12.26	10.90	100
								2.38

La distance trouvée : 2.38 est à comparer avec la valeur lue dans la table du (5% à droite) à 7-1-2=4 degrés de liberté, soit : 9.48. On ne peut donc pas rejeter l'hypothèse du raccordement.

Exercice 11

On donne dans le tableau suivant la distribution des vitesses de passage de bobines de tôle lors de l’opération de décapage (décalaminage chimique et mécanique). Ces vitesses sont en m/mn.

Raccorder cette distribution à une loi normale. On donne m = 100 et s = 20

Exercice identique au précédent.

Il faut préparer un tableau de calcul. Notez que 100 par exemple représente la classe 95-105

Exercice 12

On étudie conjointement la couleur des cheveux et celle des sourcils d’une certaine population. On les classe en deux catégories: clairs (blonds ou roux) et foncés (bruns ou noirs). On trouve les résultats suivants.

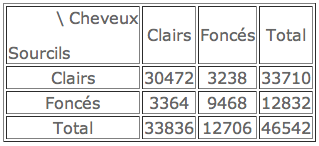
Y-a-t-il une dépendance entre la couleur des cheveux et celle des sourcils ?

Exercice 13

Dans une usine, on a remplacé la commande manuelle de quelques presses par une commande automatique. On désire voir si cette modification a une influence sur les accidents du travail. On a relevé, pendant une période donnée, le nombre d’ouvriers qui ont eu ou non des accidents et on les a classés suivant qu’ils travaillaient sur des presses à commande manuelle ou à commande automatique. On a obtenu les résultats suivants.

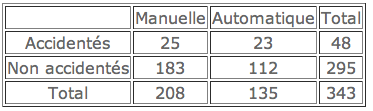
La modification du type de commande a-t-elle ou non une influence sur le nombre des accidents ?

Exercice identique au précédent.

Exercice 14

En vue d’étudier les effets du tabac sur l’artério-sclérose, on a classé 870 individus selon:

• leur degré d’artério-sclérose (grave, moyen, faible),
• leur consommation de tabac (non fumeurs, légers fumeurs, moyens fumeurs, grands fumeurs de cigarettes, fumeurs de pipe et cigares).

Analyser le tableau suivant qui a été obtenu.

Exercice identique au précédent.

On complète d'abord le tableau des effectifs observés :

Sclérose	Non fumeurs	Légers	Moyens	Grands	Pipes et cigares	∑
Grave	16	29	76	50	7	178
Moyen	97	96	180	122	42	537
Faible	48	27	32	27	21	155
∑	161	152	288	599	70	870

Puis on construit le tableau des effectifs théoriques à partir des sommes et des proportions :

Sclérose	Non fumeurs	Légers	Moyens	Grands	Pipes et cigares	∑
Grave	32.9	31.1	58.9	40.7	14.3	178
Moyen	99.4	93.8	177.8	122.8	43.2	537
Faible	28.7	27.1	51.3	35.5	12.5	155
∑	161	152	288	599	70	870

Par exemple, la première case en haut à gauche se calcule de la façon suivante :

- la proportion des non-fumeurs est : ;

- la proportion des malades graves est : ;

⇒ la proportion des non-fumeurs gravement malade est : ×× 870 =32.9

Dès lors, on peut construire le tableau des distances du () :

Sclérose	Non fumeurs	Légers	Moyens	Grands	Pipes et cigares	∑
Grave	8.71	0.14	4.95	2.12	3.74
Moyen	0.06	0.05	0.03	0.01	0.03
Faible	13.01	0	7.27	2.02	5.83
∑						48

Il y a 8 degrés de liberté. Notez que puisqu'on connaît les marges, il suffit de se donner 8 théoriques pour reconstituer tous les autres. Le à 1/1000 pour 8 degrés de liberté est égale à 26.1. Or le calculé est égal à 48 : on peut donc conclure à une influence du tabagisme sur l'artériosclérose. Notez que les plus fortes contributions au total (en gras dans le tableau) montrent moins de gravité pour les "Non fumeurs" et les "Pipes et cigares" et beaucoup plus pour les moyens fumeurs (moralité : fumez beaucoup ! ou pas du tout).

Exercice 15

Les conclusions d’une étude de la Gendarmerie sur 823 accidents graves (ayant provoqué la mort ou des blessures pour lesquelles une hospitalisation de plus de 8 jours a été nécessaire) étaient les suivantes: " Le risque d’être tué pour un passager placé à l’avant est le même que celui encouru par le conducteur, mais ce risque est presque deux fois plus élevé que pour un passager placé à l’arrière. On peut donc parler de " place du mort " pour la place occupée par le passager avant droit, mais uniquement si l’on compare le passager avant à l’ensemble des passagers, conducteur exclu. Du point de vue de la gravité des accidents, le passager avant est celui qui est le plus exposé. "

Justifier ces conclusions à partir du tableau des résultats.

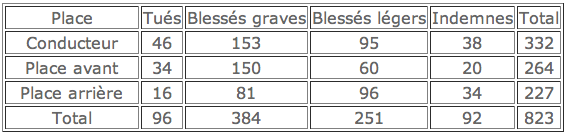
Exercice identique au précédent.