
Comparaisons statistiques
Nous présentons dans ce chapitre un raisonnement nouveau. Son inventeur, au début de ce siècle, avait pris le pseudonyme de Student. Le problème qui lui était posé était le suivant: l’engrais a-t-il une influence sur le rendement des cultures de pomme de terre ? Pour le résoudre, Student imagine de choisir 4 parcelles. Chacune d’elles est divisée en deux, et on la cultive en traitant l’une des moitiés choisie au hasard, avec de l’engrais et l’autre non. Après la récolte, on calcule les rendements et, pour une parcelle donnée, la différence de rendements entre les deux moitiés avec engrais et sans engrais. Les 4 différences obtenues sont: {11, 30, -6, 13}. Student convient de considérer ces valeurs comme des réalisations d’une variable aléatoire D. Il fait alors l’hypothèse que l’engrais n’a pas d’influence. Si cette hypothèse est vraie, la moyenne E(D) de la variable D est nulle. La démarche se poursuit par une sorte de raisonnement par l’absurde, en vérifiant si les valeurs observées peuvent être considérées comme compatibles ou non avec E(D) = 0. Si elles sont incompatibles, l’hypothèse faite doit être remise en cause, et l’on peut conclure à l’influence de l’engrais... Ce raisonnement, théorisé plus tard par Neyman et Pearson, est appelé le test d’hypothèse.
1 - Tests d'hypothèse
Théorie de Neyman et Pearson
On suppose donnée une certaine variable aléatoire X dont la loi de probabilité dépend des hypothèses que l’on désire tester. Plus précisément, on suppose qu’il existe plusieurs hypothèses H0, H1,..., Hn parfaitement connues (qui peuvent être en nombre fini ou non, dénombrable ou non) et que la loi de probabilité dépend de l’hypothèse vraie. Le test va permettre de porter un jugement sur l’hypothèse faite et d’évaluer le degré de validité du jugement, cela à partir de la valeur prise par X.
Nous étudierons d’abord le cas où l’on fait deux hypothèses simples H0 et H1. Une hypothèse est dite simple si elle définit complètement et d’une manière unique la loi de probabilité de X; sinon, elle est dite composite. C’est ainsi, par exemple, qu’en présence d’un lot de pièces distinguées en " convenables " et " défectueuses ", les deux hypothèses:
- H0: le lot contient 5 % de déchets
- H1: le lot contient 10 % de déchets
sont des hypothèses simples puisque chacune d’elles définit entièrement le lot. Tandis que les deux hypothèses:
- H0: le lot contient 5 % ou moins de 5 % de déchets
- H1: le lot contient plus de 5 % de déchets
sont des hypothèses composites puisque ni l’une ni l’autre ne définit entièrement le lot.
Supposons donc qu’il existe deux hypothèses simples H0 et H1 couvrant l’ensemble des possibilités; cela veut dire que l’une ou l’autre des deux hypothèses H0 et H1 est réalisée nécessairement. Dans ce cas, il est possible d’émettre l’un des deux jugements:
- H0 est vraie, donc H1 est fausse,
- H1 est vraie donc H0 est fausse.
On peut symboliser cet ensemble par le tableau ci-dessous où figurent, en lignes les états possibles et en colonnes les jugements portés. Le tableau contient les conséquences des différentes combinaisons.

Parmi les deux hypothèses H0 et H1, il en existe en général une dont le rejet à tort a des conséquences plus fâcheuses que pour l’autre. Il est donc normal de ne pas traiter H0 et H1 de façon symétrique. Admettant alors que H0 représente une circonstance favorable et H1 une circonstance défavorable, on peut se tromper de deux manières:
- en considérant comme défavorable ce qui est favorable; c’est l’erreur de première espèce;
- en considérant comme favorable ce qui ne l’est pas; c’est l’erreur de deuxième espèce.
C’est exactement en ces termes que se posait le problème du contrôle de réception, où ces deux types d’erreur correspondaient à des préoccupations toutes différentes: celle du fournisseur d’une part, et celle du client d’autre part.
Pour relier, maintenant, le jugement porté à l’observation de la variable X, on opère ainsi:
- on dit que H0 est vraie si la valeur observée de X, soit x, se trouve dans un certain domaine w, appelé région d’acceptation de l’hypothèse H0;
- on dit que H1 est vraie si la valeur observée n’appartient pas à w.
Pour choisir le domaine w, on impose en général deux conditions:
- que la probabilité de commettre l’erreur de première espèce soit égale à un seuil déterminé α choisi a priori aussi faible qu’on le veut;
- que la probabilité β de commettre l’erreur de deuxième espèce soit minimale.
Il importe de noter en effet que la première condition ne suffit pas, sauf cas très particulier, à définir w de façon unique.
Il est possible maintenant de compléter le tableau précédent en indiquant les règles de jugement et les probabilités pour qu’il soit correct ou faux:
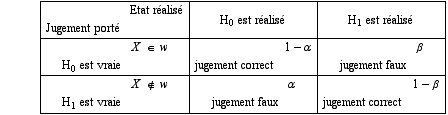
Un tel mode de raisonnement est appelé test d’hypothèse. Le complément à l’unité de β, soit (1-β) est appelé puissance du test: un test est d’autant plus puissant, pour un risque de première espèce fixé, que le risque de deuxième espèce est plus petit.
Détermination de la région d'acceptation
Si l’on note p0(x|H0) et p1(x|H1) les densités de probabilité de X, respectivement dans le cadre des hypothèses H0 et H1, les deux conditions précédentes s’expriment par les deux équations suivantes:
∫w p0(x)dx = 1-α
∫w p1(x)dx = β minimum
On démontre qu’elles sont satisfaites s’il existe une constante positive λ, telle que pour x appartenant à w:
p1(x) < λ.p0(x) (1)
sous la contrainte:
∫w p0(x)dx = 1-α (2)
La démonstration qui suit n’est pas essentielle.
Supposons qu’une telle constante λ existe et considérons la quantité:
F(w) = ∫w p1(x)dx - λ.∫w p0(x)dx
En appelant Iw(x) la fonction indicatrice du domaine w, qui prend la valeur 1 si x appartient à w et la valeur 0 sinon, on peut écrire F(w) sous la forme:
F(w) = ∫Iw(x) (p1(x) - λ.p0(x)) dx
On constate que F(w) est négatif donc minimum pour:
Iw(x)= 0 si p1(x) - λ.p0(x) ⩾ 0
Iw(x)= 1 si p1(x) - λ.p0(x) < 0
Or, lorsque F(w) est minimum sous la condition (2), la quantité ∫w p1(x)dx, c'est-à-dire β, l’est évidemment aussi. Appliquons ce résultat à deux exemples.
Test sur une proportion
Supposons qu’ayant prélevé un échantillon de n pièces dans un certain lot, on veuille tester l’hypothèse:
- H0: la proportion de déchets est ϖ0, contre l’hypothèse:
- H1: la proportion de déchets est ϖ1.
Le nombre de déchets dans l’échantillon est une variable aléatoire définie par les probabilités p0(k) si H0 est vraie et p1(k) si c’est H1:
p0(k)= Cnk ϖ0k(1-ϖ0)n-k
p1(k)= Cnk ϖ1k(1-ϖ1)n-k
La condition (1) s’écrit:
Cnk ϖ1k (1-ϖ1)n-k < λ.Cnk ϖ0k (1-ϖ0)n-k
Et, après simplification et passage aux logarithmes, on obtient:
k log(ϖ0/ϖ1) + (n-k) log(1-ϖ0/1-ϖ1) + log(λ) > 0
soit, pour ϖ1>ϖ0:
k < [n log(1-ϖ1/1-ϖ0) - log(λ)] / [log(ϖ1/ϖ0) - log(1-ϖ1/1-ϖ0)] = ks
L’inégalité se réduit donc à k < ks. Pour déterminer ks, il suffit d’utiliser la condition (2) qui s’écrit:
∑0ks Cnk ϖ0k (1-ϖ0)n-k = 1-α
On notera que la région d’acceptation ne dépend pas de la valeur ϖ1, c’est-à-dire de l’hypothèse H1. Par contre, le risque de deuxième espèce en dépend puisque:
β = ∑0ks Cnk ϖ1k (1-ϖ1)n-k
Test sur une moyenne
Soit un échantillon de taille n prélevé dans une population normale d’écart-type σ connu, mais de moyenne μ inconnue. Considérons les hypothèses:
- H0: μ=μ0
- H1: μ=μ1
La région d’acceptation est définie par:
1/[(2π)n/2σn] e-1/2 ∑i=1n (xi-μ1)²/σ² < λ/[(2π)n/2σn] e-1/2 ∑i=1n (xi-μ0)²/σ²
expression que l’on peut écrire aussi:
∑i=1n (xi-μ0)² - ∑i=1n (xi-μ1)² < 2 σ² log(λ)
soit, en notant m la moyenne empirique m = 1/n ∑i=1n xi et en supposant que μ1>μ0:
m < (μ0+μ1)/2 + [σ² log(λ)]/[n(μ1-μ0)] = ms
Pour définir ms, il suffit d’écrire que:
Prob{Mn>ms | μ=μ0} = α,
où Mn désigne la variable aléatoire moyenne d’un échantillon de taille n. Remarquons que, dans ce deuxième exemple aussi, la région d’acceptation ne dépend pas de l’hypothèse H1.
Cas d'hypothèses composites
En réalité, très souvent, le problème n’est pas de choisir entre deux hypothèses simples H0 et H1, mais entre une hypothèse simple H0 et un ensemble plus ou moins vaste d’hypothèses H1,..., Hi,..., Hn, ou même à un ensemble continu d’hypothèses H.
Dans ce cas, on peut se ramener au problème précédent en comparant successivement H0 à chacune des hypothèses de l’ensemble H. Si, par exemple, on compare H0 à Hi, la méthode exposée plus haut permet de trouver une région wi telle que le risque de première espèce soit égal à α et que le risque de deuxième espèce βi soit minimum. On obtient ainsi un ensemble de régions d’acceptation w1, ..., wi, ..., wn et, dans le cas général, on ne peut pas aller plus loin.
Mais il existe un cas particulier très intéressant, celui où les différentes régions wi ont une partie commune w. Dans ce domaine w, le test utilisé est dit uniformément le plus puissant (en abréviation de l’anglais: UMP). En effet, lorsque X tombe dans w, on est sûr que le risque de première espèce est égal à α et que le risque de deuxième espèce est minimum, quelle que soit l’hypothèse H vérifiée. Les deux exemples précédents constituent une illustration de ce cas, la région d’acceptation étant, comme nous l’avons souligné, indépendante de l’hypothèse H1. Pas tout à fait cependant: notons, en effet, que nous avons supposé, respectivement dans chacun des deux exemples, que ϖ1>ϖ0 et que μ1>μ0.
Et nous avons abouti alors à des régions d’acceptation de la forme k<ks et m<ms telles que le risque α soit bloqué à l’une des extrêmités de la distribution de la variable étudiée.
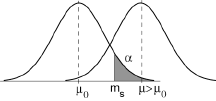
Si donc il s’agit de comparer deux hypothèses de la forme: H0: θ=θ0 et H1: θ>θ0, on est conduit à ce qu’on appelle un test à droite, où le risque de première espèce est bloqué à droite.
Le test d’hypothèses de la forme H0: θ=θ0 et H1: θ < θ0, conduit à un test appelé test à gauche.
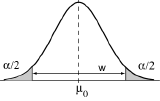
Dans le cas, enfin, d’hypothèses de la forme H0: θ=θ0 et H1: θ ≠ θ0, il apparait logique de répartir le risque α aux deux extrêmités de la distribution. Le test est alors un test symétrique.
2 - Tests usuels de comparaison à un standard
Rappel des lois outils usuelles
La détermination des régions d’acceptation nécessite la mise en oeuvre des lois de probabilité caractéristiques des échantillons prélevés dans des populations de référence spécifiées. D’où l’extrême importance d’une connaissance précise des lois de probabilité usuelles définies dans le chapitre précédent, mais que nous allons reprendre ici.
Loi normale réduite
Etant donnée une variable qui suit une loi normale de moyenne μ et d’écart-type σ, la variable:
U = (X-μ)/σ
est distribuée suivant une loi normale réduite (moyenne nulle et écart-type égal à 1).
Etant donnée la variable Mn = 1/n ∑i=1n Xi, moyenne d’un échantillon de taille n prélevé dans une population normale (μ, σ), elle suit une loi normale de moyenne μ et d'écart-type σ/√n. Il en résulte que la variable: (Mn-μ)/(σ/√n) suit une loi normale réduite.
Loi du χ²
Etant données ν variables U1, U2,... , Uν indépendantes et suivant des lois normales réduites, la variable:
χν² = U1² + U2² +...+ Uν²
suit une loi du χ² à ν degrés de liberté.
Il en résulte qu’étant donné un échantillon (X1,..., Xi,..., Xn), prélevé dans une population normale (μ, σ), la variable:
χn² = ∑i=1n [(Xi-μ)²]/σ²suit une loi du χ² à n degrés de liberté.
Appelant S² = 1/n ∑i=1n (Xi- M)² la variance de l’échantillon, la variable:
χn-1² = 1/σ² ∑i=1n (Xi-M)² = nS²/σ²suit une loi du χ² à (n-1) degrés de liberté.
Loi de Student
Etant données (ν+1) variables normales, réduites, indépendantes, la variable:
Tν = U / √[1/ν∑i=1ν Ui²]suit une loi de Student à ν degrés de liberté.
Il en résulte qu’étant données M et S² la moyenne et la variance d’un échantillon de taille n prélevé dans une population normale (μ, σ), la variable:
Tn-1 = (M-μ) / √[1/n (n.(n-1).S²)
(où n.(n-1).S² est l’estimateur sans biais de σ²) suit une loi de Student à (n-1) degrés de liberté.
Comparaison de la moyenne d’une population normale de variance s² connue à une valeur donnée µ0
Nous allons procéder en 4 étapes.
Faisons l’hypothèse que la moyenne de la population est égale à μ0:
- H0: μ=μ0, l’hypothèse alternative étant:
- H1: μ≠ μ0.
Il en résulte que la moyenne M d’un échantillon de taille n suit une loi normale de moyenne μ0 et de variance σ²/n et que, par conséquent, la variable:
U = (M-μ0)/(σ/√n)
suit une loi normale réduite.
Fixons nous un risque α que nous conviendrons de considérer comme négligeable.
Il en résulte un certain intervalle [-uα/2, uα/2] dans lequel la variable U a une probabilité (1-α) de tomber si l’hypothèse est exacte et, par conséquent, hors duquel U a une probabilité α petite de tomber. Négliger cette probabilité α, c’est considerer qu’il est impossible de trouver U en dehors de l’intervalle [-uα/2, uα/2], si l'hypothèse est vraie.
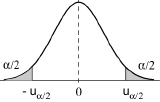
On calcule à partir des données de l'échantillon effectivement obtenu (x1,..., xn) la valeur u de U et on la situe par rapport à l'intervalle [-uα/2, uα/2]. On conclut alors de la façon suivante:
- si u tombe à l'extérieur de l'intervalle, on préfère rejeter l'hypothèse, en sachant toutefois qu'on assume le risque α de la rejeter à tort.
- si u tombe à l'intérieur de l'intervalle, cela ne signifie nullement, hélas, que l'hypothèse faite est vraie, mais seulement que les données recueillies ne sont pas en contradiction avec cette hypothèse.
Autrement dit, on est dans l'incapacité de conclure ni en faveur, ni en défaveur de l'hypothèse. On verra que dans les applications pratiques, cela est généralement moins génant qu'il n'y parait, parce que c'est contre un rejet, fait à tort, de l'hypothèse qu'il faut se prémunir, la conservation de l'hypothèse correspondant au statu quo.
Comparaison de la variance d’une population normale à une valeur donnée s0²
Faisant l’hypothèse:
H0 = σ² = σ0²
la quantité:
χ² = nS²/σ0² = 1/σ0² ∑i=1n (Xi- M)²
suit une loi du χ² à (n-1) degrés de liberté.
Il en résulte que, si l’hypothèse est vraie, nS²/σ0² a la probabilité (1-α) de tomber dans l’intervalle [χ1², χ2²] où χ1² et χ2² sont lus dans la table de la loi du χ² à (n-1) degrés de liberté. Il suffit alors, comme précédement, de calculer la valeur nS²/σ0² à partir des observations, de la placer par rapport à l’intervalle [χ1², χ2²] et enfin de conclure.
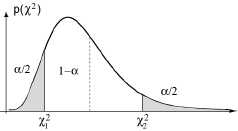
Comparaison de la moyenne d’une population normale (de variance inconnue) à une valeur donnée µ0
Faisant l’hypothèse:
H0: μ=μ0
la quantité:
T = (M-μ0) / √(S²/(n-1))
suit une loi de Student à (n-1) degrés de liberté. Le test revient à placer la quantité:
t = (m-μ0)/(σ*/√n) (où σ*² = ns²/(n-1))
par rapport à l’intervalle [-tα/2, tα/2] lu dans la table de Student à (n-1) degrés de liberté.
Tests des appariements
Nous avons présenté, dans l’introduction du chapitre, le dispositif expérimental qui consiste, disposant de n parcelles, à diviser chacune de ces parcelles en deux, et à cultiver chaque parcelle en soumettant l’une des moitiés à un certain traitement et l’autre moitié à un autre traitement. A chaque parcelle correspondront, en fin de culture, deux rendements appariés.
Imaginons un autre exemple, dans lequel on veuille confronter deux appareils de mesure et que, pour ce faire, on utilise n supports en procédant, sur chacun d’eux, à deux mesures à l’aide des deux appareils soumis à examen. Les deux mesures seront dites appariées et les résultats obtenus se présenteront, en définitive, comme suit:
mesures 1: x1, x2,..., xi,..., xn
mesures 2: y1, y2,..., yi,..., yn
Soit di la différence di = (yi - xi) et soient md et σd* la moyenne et l'écart-type estimés des différences. On admet que les di sont des réalisations d’une variable D qui suit une loi normale. Le test de l’hypothèse H0: E(D)=0 (pas d’influence du traitement ou pas de différence entre les appareils de mesures) est le test présenté au paragraphe précédent avec μ0 = 0.
3 - Comparaison sur échantillons de deux populations normales
Comparaison des variances de deux populations normales
La comparaison de deux populations normales revient à se demander si elles ont même moyenne et même variance puisque ces deux paramètres suffisent à déterminer entièrement une distribution normale. Pour des raisons théoriques qui apparaitront dans un paragraphe suivant, la comparaison des variances doit précéder celle des moyennes.
Soient n1 et s1² la taille et la variance de l’échantillon extrait de la première population, et soient n2 et s2² la taille et la variance de l’échantillon extrait de la deuxième population. Nous savons que les estimations sans biais des variances σ1² et σ2² des deux populations s’écrivent:
σ1*² = (n1.s1²)/(n1-1) et σ2*² = (n2.s2²)/n2-1
Dans l’hypothèse d’égalité des variances des deux populations: σ1² = σ2² = σ², ces deux estimations ne diffèrent qu’en raison des aléas de l’échantillonnage. Il en est de même de leur quotient f= σ1*²/σ2*² qui ne diffère de 1 qu’à cause des aléas de l’échantillonnage.
Le statisticien Snedecor, auteur du test classique que nous allons présenter, a retenu cette forme et calculé la loi de probabilité de la variable:
F(ν1,ν2) = (χ1²/ν1)/(χ2²/ν2)
où χ1² et χ2² sont deux variables aléatoires indépendantes qui suivent des lois du χ² à ν1 et ν2 degrés de liberté.
Dans l’hypothèse d’égalité des variances des deux populations, si l’on désigne par S1² et S2² les variables, dont les variances des échantillons qui en sont extraits au hasard, sont des réalisations, n1S1²/σ² et n2S2²/σ² sont indépendantes et suivent des lois du χ² à (n1-1) et (n2-1) degrés de liberté. Il en résulte, par définition de cette variable, que le quotient:
F = [n1S1²/n1-1] / [n2S2²/n2-1]
suit une loi de Snedecor à (n1-1) et (n2-1) degrés de liberté. Par conséquent, la quantité:
f= σ1*²/σ2*²
est une réalisation, si l’hypothèse d’égalité des variances est vérifiée, d’une loi de Snedecor.
Cette loi définie, la suite des opérations est maintenant bien connue. Se fixant un seuil de probabilité α négligeable, on lit dans la table de Snedecor à (n1-1) et (n2-1) degrés de liberté les valeurs f1 et f2 correspondant au dessin ci-dessous.
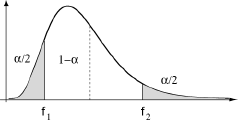
Estimation de s²
En admettant que le résultat du test précédent ne s’oppose pas à l’hypothèse d’égalité des variances, il peut s’avérer utile d’estimer la valeur commune σ² des variances des deux populations.
Puisque n1S1²/σ² et n2S2²/σ² sont des variables indépendantes qui suivent des lois du χ², respectivement à (n1-1) et (n2-1) degrés de liberté leur somme (n1S1²+n2S2²)/σ² suit une loi du χ² à (n1+n2-2) degrés de liberté, dont la moyenne et la variance sont respectivement (n1+n2-2) et 2(n1+n2-2).
Il en résulte que la variable (n1S1²+n2S2²)/(n1+n2-2) est un estimateur sans biais et convergent de σ², puisque
E[(n1S1²+n2S2²)/(n1+n2-2)] = σ² et
σ²[(n1S1²+n2S2²)/(n1+n2-2)] = 2σ4/(n1+n2-2) → 0.
Par conséquent, la quantité:
σ*² = (n1s1²+n2s2²)/(n1+n2-2)
calculée à partir des observations, est une estimation sans biais de σ².
Comparaison des moyennes de deux populations normales
Dans l’hypothèse de populations normales, une fois testée l’égalité des variances, il suffit de tester l’égalité des moyennes pour pouvoir considérer que les populations sont identiques. Les raisons théoriques qui conduisent à présenter la comparaison des variances avant celle des moyennes peuvent, à ce stade, être explicitées. En effet, le test de comparaison des variances ne faisait aucune hypothèse sur l’égalité des moyennes. Par contre, le test d’égalité des moyennes implique l’égalité des variances. Il est donc nécessaire de vérifier cette égalité avant de s’intéresser aux moyennes.
Cela étant, soient deux populations normales P1 et P2 de moyennes μ1 et μ2, mais de même variance σ². Soient n1 et n2 les tailles de deux échantillons ℰ1 et ℰ2 prélevés au hasard respectivement dans chacune de ces deux populations; soient m1 et m2 leurs moyennes, et soient s1² et s2² leurs variances.
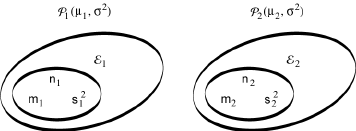
Dans ces conditions, il est permis de considérer que:
- m1 est une réalisation d’une variable M1 normale, de moyenne μ1 et de variance σ²/n1,
- m2 est une réalisation d’une variable M2 normale, de moyenne μ2 et de variance σ²/n2,
- s1² et s2² sont des réalisations de variables S1² et S2² telles que la variable (n1S1² + n2S2²)/σ² suit une loi du χ² à (n1+n2-2) degrés de liberté et est indépendante de M1 et M2.
Faisons maintenant l’hypothèse que μ1=μ2=μ. Il en résulte que la variable (M1 - M2) suit une loi normale de moyenne nulle et de variance égale à la somme des variances de M1 et M2, c’est-à-dire à σ²(1/n1 + 1/n2). Par conséquent, la variable:
U= (M1-M2)/(σ√(1/n1+1/n2))
suit une loi normale réduite.
Pour éliminer la quantité σ inconnue, il suffit de considérer le quotient:
T = 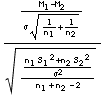 =
= 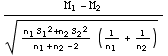
qui suit une loi de Student à (n1+n2-2) degrés de liberté. Pour simplifier l’écriture, on peut tenir compte de ce que figure, au dénominateur, l’expression de l’estimateur sans biais de σ². Par conséquent t = (m1-m2)/(σ*√(1/n1+1/n2) est une réalisation d’une loi de Student qu’il suffit, pour conclure, de placer par rapport à l’intervalle [-tα/2, tα/2] correspondant au risque α choisi.
Si t n’appartient pas à l’intervalle, on dit souvent que la différence entre les moyennes observées est significative au risque α et, sinon, qu’elle n’est pas significative.
Estimation de la différence des moyennes des populations
Si la différence observée entre les moyennes m1 et m2 des échantillons est significative (d’une différence entre les moyennes μ1 et μ2 des populations), il peut s’avérer utile d’estimer la différence Δ=μ1-μ2. La variable (M1-M2) est évidemment un estimateur sans biais de Δ. Quant à la détermination de l’intervalle de confiance, elle repose sur la prise en compte de la variable:
T = 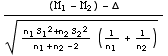
qui suit une loi de Student à (n1+n2-2) degrés de liberté.
On a, par conséquent, au risque α près:
(m1-m2) - tα/2 σ*√(1/n1+1/n2) < Δ < (m1-m2) + tα/2 σ*√(1/n1+1/n2)
Exercices
Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !
Exercice 1
On a prélevé, au hasard dans une population normale de moyenne μ et d’écart-type σ, un échantillon de taille n=10. La moyenne et la variance calculées sur cet échantillon sont respectivement m=4 et s²=6.
- Calculer une estimation sans biais de σ et son intervalle de confiance au risque 5%.
- Tester l’hypothèse σ=2 au risque 5%.
- En admettant σ connu égal à 2, tester l’hypothèse μ=3 au risque 5%.
- Tester, au risque 5%, l’hypothèse μ = 3 sans faire aucune hypothèse sur la valeur de σ.
- Calculer une estimation sans biais de μ et son intervalle de confiance au risque 5% sans faire aucune hypothèse sur la valeur de σ.
- En admettant μ connu égal à 3, est-il possible d’envisager un test plus efficace que celui mis en oeuvre en b) pour tester l’hypothèse σ=2 ?
Cet exercice permet de poser les notions du chapitre et de faire le lien avec le chapitre 4.
En particulier, ne pas confondre intervalle de confiance d'une variable (questions a, e, cf. chapitre 4) et test d'hypothèse (questions b, c, cf. ce chapitre).
Exercice 2
Pour comparer les rendements de deux variétés de blé A et B, on a ensemencé 10 couples de deux parcelles voisines, l’une en variété A, l’autre en variété B, les 10 couples étant répartis dans des localités différentes. On a obtenu les résultats suivants:

Que peut-on conclure de ces résultats (Au risque alpha=5%)?
Calcul des paramètres
Moyenne échantillon
Variance échantillon
Écart-type empirique
Exercice sur les appariements. On va travailler sur la variable différence entre les 2 récoltes.
Exercice 3
On donne ci-après les pourcentages de matière grasse dans un aliment, déterminés sur 10 échantillons par deux méthodes d’analyse différentes A et B.

Comparer ces deux méthodes au risque alpha = 5%.
Calcul des paramètres
Moyenne échantillon
Variance échantillon
Écart-type empirique
Exercice sur les appariements, identique dans son raisonnement au 5.2. On va travailler sur la variable différence entre les 2 résultats.
Exercice 4
On a prélevé au hasard un échantillon ℰ1 de taille n1 = 10 dans une population normale P1 de moyenne μ1 et d’écart-type σ1. La moyenne et la variance calculées sur cet échantillon sont respectivement m1 = 4 et s1² = 6.
On préleve au hasard un échantillon ℰ2 de taille n2 = 15 dans une population normale P2 de moyenne μ2 et d’écart-type σ2. La moyenne et la variance calculées sur cet échantillon sont respectivement m2 = 7 et s2² = 20.
- Tester l’hypothèse σ2 = σ1, au risque 5%.
- Tester l’hypothèse σ2 = 2σ1, au risque 5%.
- En admettant que σ2 = 2σ1, calculer une estimation sans biais de σ1, à partir des deux échantillons, et son intervalle de confiance au risque 5%.
- Utiliser un test du χ² pour tester simultanément les hypothèses σ² =4 et σ1 =2.
- En admettant que σ2 = 2σ1 = 4, tester, au risque 5%, l’hypothèse μ2 = 2μ1.
- Calculer une estimation de μ1 à partir des deux échantillons, en admettant que μ2 = 2μ1 et son intervalle de confiance au risque 5%.
a) hypothèse σ2 = σ1, au risque 5%.
Estimation variance 1
Estimation variance 2
Réalisation Snédécor
Paramètre Snédécor
b) hypothèse σ2 = 2σ1, au risque 5%.
Réalisation Snédécor
Paramètre Snédécor
Questions c à f
Voir solution
Comme le 5.1, cet exercice permet de poser les notions du chapitre et de faire le lien avec le chapitre 4. En particulier, ne pas confondre intervalle de confiance d'une variable et test d'hypothèse. Pour un exercice paramétré, voir exercice 5.1.
Exercice 5
Il y a des raisons de penser que l'épaisseur de la cire dont sont enduits des sacs en papier est plus irrégulière à l'intérieur qu'à l'extérieur. Pour le vérifier 75 mesures de l'épaisseur ont été faites et ont donné les résultats suivants:
- surface intérieure: ∑x=71.25 et ∑ x2 =91
- surface extérieure: ∑y=48.75 et ∑ y2 =84.
- Faire un test pour déterminer, au risque 5%, si la variabilité de l'épaisseur de la cire est plus grande à l'intérieur qu'à l'extérieur des sacs.
- Revenant à la loi de F, calculer l'intervalle de confiance à 95% du rapport des variances.
a) hypothèse σ2 = σ1, au risque 5%.
Estimation variance x
Estimation variance y
Paramètre Snédécor
b) Voir Solution
Exercice faisant appel à la loi de Snedecor. Dans le b), il faudra se ramener à la loi de F, cf. poly.
Exercice 6
Deux chaines de fabrication produisent des transistors. Des relevés effectués pendant 10 jours ont donné les résultats suivants:
- ligne 1: mx=2800 et ∑ (x-mx)²=103600
- ligne 2: my=2680 et ∑ (y-my)²=76400
On admettra que les écarts-type σx et σy sont inconnus mais égaux.
- Peut-on conclure, au risque de 5%, à une différence entre les productions moyennes des deux lignes ?
- Quel est l'intervalle de confiance à 95% de la différence ?
Il s'agit de la comparaison de deux distributions normales à partir de deux échantillons qui en sont issus. Ici, pas besoin de tester d'abord les écarts-types, on calcule la valeur d'un estimateur commun puis on testera l'hypothèse d'égalité des moyennes.

![[Graphics:HTMLFiles/index_16.gif]](HTMLFiles/index_16.gif)
![[Graphics:HTMLFiles/index_33.gif]](HTMLFiles/index_33.gif)
![[Graphics:HTMLFiles/index_37.gif]](HTMLFiles/index_37.gif)
![[Graphics:HTMLFiles/index_77.gif]](HTMLFiles/index_77.gif)
![[Graphics:HTMLFiles/index_101.gif]](HTMLFiles/index_101.gif)
![[Graphics:HTMLFiles/index_165.gif]](HTMLFiles/index_165.gif)
![[Graphics:HTMLFiles/index_303.gif]](HTMLFiles/index_303.gif)
![[Graphics:HTMLFiles/index_310.gif]](HTMLFiles/index_310.gif)