Le Contrôle Statistique
Le contrôle de la qualité constitue sans doute le poste le plus important de l'entreprise moderne. Les méthodes de fabrication à la chaîne exigent une parfaite interchangeabilité entre les innombrables pièces fabriquées en série. Un tel résultat ne peut être atteint que si les spécifications imposées sont rigoureusement respectées. A ce premier objectif de qualité s'en ajoute un second qui semble s'opposer au précédent, celui de l'économie. La qualité voudrait qu'on se livre à un examen minutieux de la fabrication ; l'économie exige qu'on réduise au maximum tous les frais, en particulier ceux du contrôle qui peuvent constituer une part très importante du prix de revient. Cela fait apparaître la nécessité de substituer à une inspection à 100% des pièces fabriquées, un contrôle par échantillonnage, ou contrôle statistique qui devient d'ailleurs inévitable lorsqu'on doit procéder à des essais destructifs : résistance des matériaux, par exemple. Il importe, dès lors, de rechercher des modes de contrôle qui permettent à la fois de prélever un nombre de pièces aussi faible que possible, et de déterminer aussi bien que possible la qualité d'un lot.
1 - Distribution D'échantillonnage
Population
En statistique, on appelle population un ensemble d'éléments caractérisés par un critère permettant de les identifier sans ambiguïté. Chacun des éléments est appelé individu. Ces appellations sont liées aux origines démographiques de la statistique. On parlera, par exemple, de la population des axes usinés sur telle machine-outil pendant telle période, en s'intéressant d'ailleurs, non pas aux individus en tant que tels, mais à une ou plusieurs de leurs caractéristiques.
Chacune des caractéristiques sur laquelle on décide de faire porter l'observation est appelée variable (ou caractère). Il importe de faire ici une distinction entre deux types de variables et par conséquent, deux catégories de populations :
- Populations à caractéristiques qualitatives. Pour des axes, par exemple, on distinguera entre pièces satisfaisantes et pièces défectueuses. On se trouve dans ce cas chaque fois qu'un contrôle s'effectue par calibre, c'est-à-dire que l'on distingue, par exemple, les axes dont le diamètre appartient ou n'appartient pas à un certain intervalle admissible appelé intervalle de tolérance.
- Populations à caractéristiques quantitatives (ou mesurables). Dans l'exemple des axes, on peut mesurer le diamètre des axes et classer les pièces suivant les valeurs qu'il peut prendre.
La notion de population n'est pas toujours très facile à définir avec précision. Si on considère, par exemple, la production journalière d'une machine-outil, on peut, de prime abord, parler de la population des pièces produites ; mais, au cours de la journée, la machine a pu se dérégler, l'ouvrier qui surveille la fabrication a peut-être procédé à un réglage, etc. Il n'est donc pas du tout évident que l'ensemble de la production journalière constitue une population unique et bien homogène.
Un autre type de difficulté peut se présenter pour définir la population. Supposons, par exemple, que la variable étudiée soit la résilience de l'acier des lingots d'une certaine coulée. L'individu, c'est-à-dire l'élément sur lequel on effectue la mesure est une éprouvette d'acier découpée et usinée suivant certaines modalités. Pour définir la population, il faut se référer à l'ensemble infini de toutes les éprouvettes susceptibles d'être réalisées dans les mêmes conditions à partir des lingots étudiés.
Echantillon
Une partie essentielle de la statistique, consiste à porter des jugements sur une population à partir d'échantillons ; c'est ce qu'on appelle l'inférence statistique. Un échantillon est un ensemble d'individus prélevés, suivant un procédé bien défini, dans l'ensemble plus important constitué par la population. Le nombre d'individus prélevés s'appelle la taille de l'échantillon, que nous noterons généralement n. Tous les résultats statistiques établis sur les échantillons impliqueront que ces derniers sont représentatifs de la population dont ils proviennent. C'est le cas s'ils ont été prélevés au hasard, c'est à dire que tous les individus de la population avaient la même probabilité de faire partie de l'échantillon effectivement prélevé. En pratique, l'obtention d'échantillons au hasard présente un certain nombre de difficultés qui peuvent être levées si l'on peut numéroter chacun des individus de la population et qu'on a alors recours à une table de nombres au hasard.
Dans toute la suite, nous admettrons que les échantillons sont prélevés de façon non exhaustive ou bien que la taille de la population est suffisamment importante devant celle de l'échantillon pour que l'on puisse se ramener à ce cas.
red
Caractéristiques Des Échantillons
Nous désignerons par la notation x1, x2,... , xi ,... , xn, les valeurs prises par la variable pour chacun des individus constituant l'échantillon, ce qu'on appelle une série d'observations. Les séries d'observations peuvent être caractérisées par un certain nombre de valeurs typiques que nous allons définir.
Caractéristiques de tendance centrale
On appelle caractéristique de tendance centrale, une fonction des observations dont la valeur est comprise entre les valeurs extrêmes de la série. La plus couramment utilisée est la moyenne arithmétique :
m = 1/n ∑i=1n xiqui est très facile à calculer et possède d'importantes propriétés théoriques, par ailleurs assez faciles à établir. La moyenne, toutefois, possède l'inconvénient d'être très sensible au retrait ou à l'ajout d'une observation "aberrante" : on dit que c'est une statistique peu robuste.
Une caractéristique de tendance centrale plus robuste est la médiane dont les propriétés théoriques, par contre, sont plus compliquées à manipuler que pour la moyenne. Lorsqu'on a classé les observations par ordre de grandeurs croissantes, la médiane est la valeur de l'observation qui se trouve au rang (n+1)/2 , si n est impair. Si n est pair (n = 2p), c'est le milieu de l'intervalle [xp, xp+1].
De façon plus générale, on définit les quantiles. Par exemple les déciles : le premier décile est la valeur telle qu'il y ait 10 % des observations en dessous d'elle, le neuvième décile est la valeur telle qu'il y ait 10 % des observations au dessus d'elle. De même, les quartiles : le premier et le troisième quartiles laissent respectivement 25 % et 75 % des observations en dessous d'eux et la médiane est donc le deuxième quartile.
Caractéristiques de dispersion
On appelle caractéristique de dispersion, une fonction des observations dont la valeur rend compte du plus ou moins grand étalement des valeurs observées autour de leur tendance centrale. On appelle étendue w d'une série d'observations, l'écart entre la plus grande et la plus petite valeur de la série :
w = xmax- xmin
dont le principal avantage est la simplicité de calcul, mais qui est, par contre, extrêmement peu robuste.
On appelle variance s² d'une série d'observations, la quantité qui est définie par la relation :
s² = 1/n ∑i=1n (xi-m)²et qui mesure l'écart moyen quadratique entre les observations et leur moyenne. Elle joue un rôle très important dans toute la statistique mathématique. Pour la calculer, on notera l'incontournable relation :
s² = 1/n (∑i=1n xi² - 2m ∑i=1n xi +n m²) = 1/n ∑i=1n xi² - m²
que l'on mémorisera facilement en retenant que :
la variance est égale à la moyenne des carrés moins le carré de la moyenne
.La racine carrée s de la variance est appelée l'écart-type :
s = √(1/n ∑i=1n (xi-m)²)
Variance et écart-type sont assez peu robustes. Plus favorable, de ce point de vue, on peut calculer l'écart absolu moyen e des observations à leur moyenne :
e = 1/n ∑i=1n |xi-m|Enfin, une caractéristique de dispersion extrêmement robuste est la distance interquartile : écart entre le troisième quartile Q 3 et le premier quartile Q1 :
IQ = Q3 - Q1
Distribution D'échantillonnage
On appelle population de référence ou modèle, une population définie par une loi de probabilité P(x) pouvant être considérée comme à l'origine des résultats observés, c'est-à-dire telle que la probabilité pour que la variable étudiée prenne une valeur dans un certain intervalle [x, x + h[, pour un individu prélevé au hasard, soit :
Prob{x ≤ X < x+h} = P(x+h) - P(x)
Cela étant, considérons une population de référence définie par la loi de probabilité d'une certaine variable aléatoire X. Si nous prélevons, au hasard et de façon non exhaustive, un échantillon de taille n, nous observons n valeurs :
x1, x2, ... , xi, ... , xn
dont on peut calculer la moyenne m et la variance s². Mais un autre échantillon de taille n, prélevé au hasard dans la même population, conduirait à d'autres valeurs :
x'1, x'2, ... , x'i, ... , x'n
puis m' et s'² , a priori différentes à cause des fluctuations dues à l'échantillonnage ... Et ainsi de suite, on pourrait répéter ces mesures et ces calculs sur un grand nombre d'échantillons différents.
Les nombres x1, x'1, ... peuvent alors être considérés comme des réalisations d'une certaine variable aléatoire X1, les nombres x2, x'2, ... comme des réalisations d'une variable aléatoire X2, et plus généralement, les nombres xi, x'i, ... comme des réalisations d'une variable aléatoire Xi.
Les variables aléatoires X1, X2, ..., Xi, ... sont indépendantes (si l'échantillonnage est non exhaustif) et ont même loi de probabilité : celle qui définit la population de référence.
Les valeurs m, m', ... peuvent alors être considérées comme des réalisations d'une variable aléatoire Mn , fonction des variables aléatoires X1, X2, ... , Xi, ... Xn:
Mn = 1/n ∑i=1n Xi
La distribution de Mn est appelée distribution d'échantillonnage. Il en est de même de celle de la variable aléatoire :
Sn² = 1/n ∑i=1n (Xi-Mn)²
La détermination des lois d'échantillonnage est fondamentale en statistique. Nous avons déjà étudié une de ces lois : la loi binomiale qui se rencontre chaque fois que l'on étudie un lot de pièces contenant une proportion ϖ de pièces défectueuses et qu'on y prélève, de façon non exhaustive, un échantillon de n pièces. Le nombre Knde pièces défectueuses contenues dans l'échantillon est une variable aléatoire qui peut prendre les valeurs 0, 1, ... , k, ... , n avec les probabilités :
Prob{Kn = k} = Cnk ϖk (1-ϖ)n-k
La suite fournira plusieurs exemples de lois d'échantillonnage. Nous nous limiterons, dans ce chapitre, à un autre cas particulier concernant, cette fois, une population à caractéristique quantitative.
Distribution De La Moyenne D'un Échantillon Prélevé Dans Une Population Normale
On rencontre très fréquemment, dans la pratique, des populations à caractéristiques quantitatives qui peuvent être raccordées à des populations de référence définies par une loi de probabilité normale :
Prob{X≤x} = 1/(σ.√(2π)) ∫-∞x e-1/2 ((u-μ)/σ)²du
On dit alors que la population est normale de moyenne μ et d'écart-type σ. Considérons la variable aléatoire Mn : moyenne d'un échantillon prélevé au hasard dans une telle population :
Mn = (X1 + X2 + ... + Xn)/n
On a établi qu'une somme de variables indépendantes, suivant des lois normales, suivait elle-même une loi normale de moyenne égale à la somme des moyennes des variables, et de variance égale à la somme de leurs variances. Il en résulte que Mn suit une loi normale de moyenne :
E[Mn]= (E[X1] + E[X2] + ... + E[Xn])/n = μ
et de variance :
σ²[Mn]= (σ²[X1] + σ²[X2] + ... + σ²[Xn])/n² = σ²/n
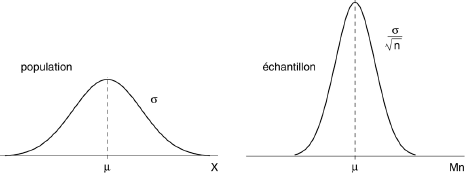
On peut encore écrire ce résultat très important :
Prob{ |Mn-μ| > u.σ/√(n) } = 2/√(2π) ∫u+∞ e-t²/2 dt
2 - Contrôle Statistique
Contrôle De Fabrication Et Contrôle De Réception
Nous appellerons qualité ω d'un lot, la proportion de pièces défectueuses qu'il contient. La qualité d'une pièce peut, quant à elle, être déterminée, suivant les cas, de deux manières :
- contrôle qualitatif : la pièce est passée au calibre et l'on vérifie si elle correspond ou non aux tolérances imposées par le cahier des charges ;
- contrôle quantitatif : la pièce est mesurée, et l'on vérifie si la valeur obtenue est comprise dans l'intervalle de tolérance.
On distingue encore deux types de contrôle :
- contrôle de fabrication : c'est celui qui est effectué à chaque stade de l'élaboration d'un produit pour limiter la proportion de rebuts ;
- contrôle de réception : c'est celui qui est effectué par le client qui achète une certaine quantité de ce produit et veut vérifier que sa qualité correspond bien à ce qu'il attend.
En fait, leurs méthodes reposent sur les mêmes bases. Nous nous limiterons donc à l'étude du contrôle de réception dans le cas qualitatif, et à celle du contrôle de fabrication dans le cas quantitatif.
Contrôle De Réception
L'objectif du contrôle, dans ce cas, est de porter un jugement sur la proportion ω inconnue de pièces défectueuses contenues dans un lot. En général, deux parties se trouvent en présence, un fournisseur et un client, dont les exigences peuvent se traduire de la façon suivante :
- le fournisseur ne voudrait pas qu'on lui refuse un lot contenant ω1 ou moins de déchets ;
- le client ne voudrait pas accepter un lot s'il contient ω0 ou plus de déchets.
Il faut remarquer dès ce stade que ω1 et ω0 sont définis à partir de considérations techniques et non statistiques. Le fournisseur peut déterminer ω1 en fonction de son matériel, de son prix de vente, etc. Le client détermine ω0 en fonction des conséquences économiques ou techniques qu'entraîne pour lui la présence de pièces défectueuses dans les lots réceptionnés.
Définir une règle de contrôle, va consister à fixer la taille n de l'échantillon à prélever, et une valeur limite c telle que :
- si on trouve moins de c pièces défectueuses parmi les n pièces prélevées, on accepte le lot ;
- si on en trouve plus de c, on le refuse.
Examinons les conséquences d'une telle règle. Connaissant n et c, il est possible, par référence à la loi binomiale, de calculer la probabilité P(ω) d'accepter un lot où la proportion de pièces défectueuses serait égale à une valeur ω donnée quelconque :
P(ϖ) = ∑k=0c Cnk ϖk(1-ϖ)n-k
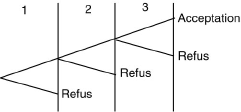
P(ω) varie avec ω. La courbe représentative de la fonction P(ω) est appelée la courbe d'efficacité de la règle de contrôle.
Elle a la forme indiquée ci-après. Si l'on compare les courbes 1 et 2, on constate que la règle relative à la courbe 2 est plus sévère que celle qui correspond à la courbe 1, la probabilité d'accepter un lot de qualité donnée ω, étant plus faible: on dit qu'elle est plus efficace.
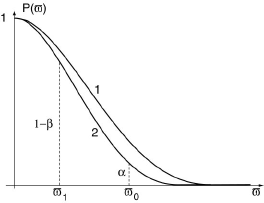
On constate, d'autre-part, qu'à une règle donnée correspond :
- une probabilité α d'accepter un lot présentant une proportion ω0 de déchets ; c'est le risque du client ;
- une probabilité β de refuser un lot présentant une proportion ω1 de déchets ; c'est le risque du fournisseur.
Il en résulte qu'il est possible inversement de déterminer la règle du contrôle, c'est à dire n et c, telle que la courbe d'efficacité passe par les deux points {ω0, α} et {ω1, 1-β}, à partir des deux relations :
α = ∑k=0c Cnk ϖ0k (1-ϖ0)n-k
1-β = ∑k=0c Cnk ϖ1k (1-ϖ1)n-k
Il est clair qu'aussi petits soient-ils choisis, les risques α et β devront être consentis par le fournisseur et le client.
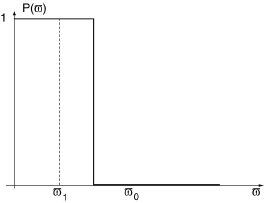
A la limite en effet, la courbe d'efficacité qui conduirait à accepter avec certitude tout lot contenant une proportion de déchets inférieure à ω1 et à refuser avec certitude tout lot contenant une proportion de déchets supérieure à ω2, devrait avoir la forme indiquée ci-après. Seule une inspection à 100 % permettrait de l'obtenir.
Contrôle En Cours De Fabrication
Intervalle de tolérance et déchets
Considérons les pièces usinées sur un tour automatique. Si l'on s'intéresse au diamètre de ces pièces, on constate que, pour un certain réglage de la machine, c'est une variable aléatoire que l'on peut mettre sous la forme :
D = μ + σ U,
où μ est un nombre certain, U une variable normale centrée et réduite, et où σ correspond à la variabilité de la machine et en constitue une caractéristique intrinsèque pour un certain niveau d'usure. La machine sera réglée au mieux si μ est égal à la cote théorique μ0 prévue pour la pièce.
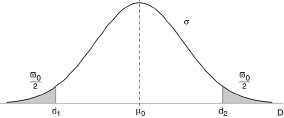
Mais, même si le réglage représente ce qu'on peut obtenir de mieux sur la machine, dans l'état où elle se trouve, il n'empêchera pas pourtant la production d'une proportion ϖ0 de pièces défectueuses, c'est-à-dire dont le diamètre sort des limites de tolérance [d1, d2] :
ϖ0 = 2 Prob{U > (d2-d1)/2σ }
où U suit une loi normale réduite. On constate que ϖ 0 est d'autant plus grand que σ l'est devant l'intervalle de tolérance.
Règle de contrôle
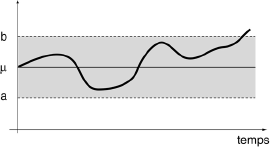
Le principe du contrôle en cours de fabrication est de prélever à intervalles réguliers n pièces consécutives, de calculer leur moyenne et de vérifier qu'elle tombe à l'intérieur d'un certain intervalle :
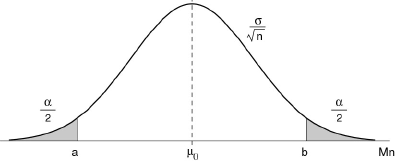
[a,b]=[ μ0 - uα/2 σ/√n , μ0 + uα/2 σ/√n ]
uα/2 désignant la valeur d'une variable normale réduite U, correspondant à la probabilité α telle que :
α = 2 Prob{U > uα/2 }
Efficacité d'un contrôle
Si la moyenne calculée tombe dans l'intervalle [a, b], on laisse la fabrication se poursuivre ; sinon, on règle la machine. α représente donc le risque de procéder à un réglage de la machine alors qu'elle n'est pas déréglée. C'est la probabilité conditionnelle :
α = Prob{ Mn ∉ [a,b] | μ=μ0 }
Supposons maintenant que la machine se dérègle et que la moyenne de la fabrication devienne μ ≠ μ0. On peut calculer la probabilité :
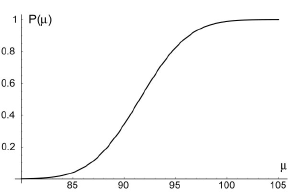
P(μ) = Prob{ Mn ∈ [a,b] | μ}
qui désigne le risque de laisser la fabrication se poursuivre alors que la machine est déréglée. On a évidemment:
P(μ0) = 1-α
La courbe représentative de la fonction P(μ) est appelée courbe d'efficacité du contrôle. Pour un risque α donné, l'efficacité croît avec n : on a d'autant plus de chances de détecter un déréglage donné |μ-μ0| que les échantillons prélevés sont plus importants.
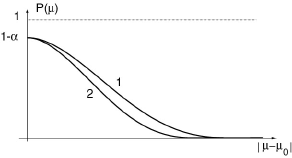
Risque β
Considérons maintenant la valeur μ 1 de μ qui correspond à une proportion ϖ 1 de déchets, que l'on considère comme inadmissible parce que trop importante, et qui est déterminée à partir de considérations techniques et (ou) économiques.
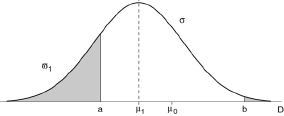
Remarquons que la valeur μ'1 qui est symétrique de μ1 par rapport à μ0 (milieu de l'intervalle de tolérance) correspond au même déréglage |μ-μ0| et conduit à la même proportion ϖ1 de déchets.
Ayant ainsi déterminé μ1, on note généralement β la probabilité P(μ1) qui est le risque de ne pas régler la machine alors que son déréglage est inadmissible :
β = Prob{Mn ∈[a,b] | μ=μ1}
Choix de la taille de l'échantillon à prélever
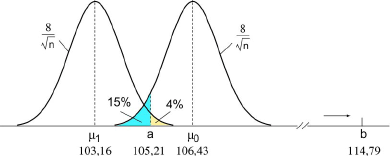
Il peut dès lors s'avérer intéressant, au lieu de fixer au départ n et α, de se fixer α et β, et d'en déduire la règle de contrôle, c'est-à-dire n et [a, b], de telle sorte que la courbe d'efficacité passe par les deux points {μ0, 1-α} et {μ1, β}.
La figure suivante illustre les deux relations qui permettent de mener facilement les calculs :

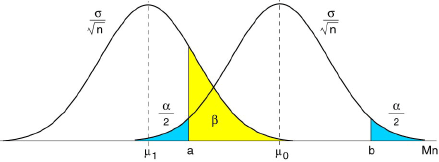
Le calcul pratique peut être notablement simplifié en tenant compte du fait que la probabilité :
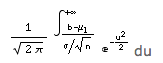
est presque toujours négligeable et que l'on peut écrire, par conséquent:
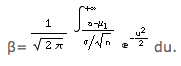
Contrôle Progressif
Les règles de contrôle que nous venons d'envisager consistaient, dans le cas qualitatif par exemple, à :
- prélever dans le lot un échantillon de n pièces que l'on examine une à une,
- accepter le lot si on trouve c ou moins de c pièces défectueuses, sinon le refuser.
Il peut être judicieux d'envisager d'autres types de règles de contrôle, telles que l'on accepte le lot si le résultat d'un premier échantillon est bon, qu'on le refuse si ce résultat est mauvais, et qu'on examine un deuxième échantillon si ce résultat est moyen, de manière à confirmer d'une façon ou d'une autre la première opinion qu'on avait pu former. Une telle règle peut s'énoncer ainsi :
- prélever un échantillon de n1 pièces,
- si on trouve c1 ou moins de c1 pièces défectueuses, accepter le lot ; si on en trouve c2 ou plus de c2, refuser le lot ; si on en trouve entre c1 et c2, prélever un nouvel échantillon de n2 pièces;
- si le nombre total de pièces défectueuses trouvées dans les deux échantillons est inférieur ou égal à c3, accepter le lot ; le refuser dans le cas contraire.
Il s'agit là de ce qu'on appelle un plan d'échantillonnage double. On peut utiliser aussi des plans d'échantillonnage multiples où l'on prélève plus de deux échantillons. L'avantage des plans multiples réside dans le fait que, pour une efficacité donnée, ils conduisent à un nombre moyen de pièces prélevées inférieur au nombre de pièces prélevées dans le plan simple équivalent.
Les plans multiples conduisent, à la limite, aux plans progressifs. Dans ce cas, l'effectif de l'échantillon n'est pas précisé à l'avance. On prélève les pièces une à une et, à chaque stade, on calcule le nombre total kn de pièces défectueuses. Suivant la valeur de kn, on accepte le lot, ou on le refuse, ou bien on prélève une (n+1)ème pièce.
Exercices
Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !
Exercice 1
Pour contrôler un lot important d'articles, on adopte la règle suivante :
- on prélève un article au hasard; s'il est mauvais on refuse le lot ; s'il est bon, on prélève un deuxième article.
- si le deuxième article est mauvais, on refuse le lot ; s'il est bon, on prélève un troisième article.
- si le troisième article est mauvais, on refuse le lot ; s'il est bon, on accepte le lot.
- Calculer la probabilité de refuser le lot et l'espérance du nombre d'articles prélevés, en fonction de la proportion d'articles défectueux dans le lot.
- Comparer ces résultats à ceux que l'on aurait obtenus en prélevant directement trois articles, et en refusant le lot si l'un d'eux au moins est mauvais.
Cet exercice nous permet d'introduire le principe du contrôle progressif, fréquemment utilisé en usine. Commencez par faire l'arbre de décision afin de bien cerner les différents cas possibles. Une fois cela effectué, établissez la loi du nombre de pièces prélevées (X) et calculez son espérance. Trouvez la valeur maximale prise par l'espérance et comparez la à l'espérance du nombre de pièces prélevées avec le second test.
Exercice 2
Une entreprise réceptionne périodiquement des lots de pièces d'un certain type destinées à entrer dans des assemblages. On suppose que les conditions d'utilisation de ces pièces rendent souhaitable le rejet d'un lot contenant une proportion de déchets supérieure à 8%.
- On décide d'adopter la règle suivante : on prélève 100 pièces que l'on examine une à une, et on compte le nombre k de pièces défectueuses ; si ce nombre est inférieur ou égal à 3, on accepte le lot ; dans le cas contraire, on le refuse. En admettant l'approximation de Poisson, quelle est la limite supérieure du risque d'accepter un lot contenant plus de 8% de déchets ?
- Le fournisseur souhaiterait ne pas se voir refuser des lots qu'il estime éminemment convenables lorsqu'ils contiennent moins de 3% de déchets. Quel risque maximum encoure-t-il avec la règle précédente ?
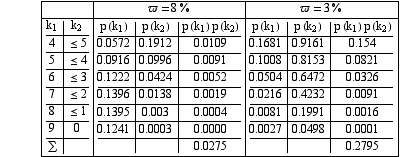
- Que deviennent les 2 risques précédents si l'on prélève 200 pièces et que l'on fixe comme limite d'acceptation k <= 9 ?
On adopte un plan d'échantillonnage multiple défini de la façon suivante :
- on prélève 100 pièces. Si k1 <= 3, on accepte le lot; si k1 > 9, on le refuse ;
- si 3 < k1 <= 9, on prélève à nouveau 100 pièces. Si k1 + k2 <= 9, on accepte le lot ; sinon on le refuse.
Comparer son efficacité au précédent. Quelle est l'espérance mathématique du nombre de pièces prélevées ?
Réponse A (Prob(k<=3, ω=8%))
Réponse B Prob(k>3, ω=3%)
Réponse C1 (Prob(k<=3, ω=8%))
Réponse C2 (Prob(k>3, ω=3%))
Réponse D1 (Prob(ω=8%))
Réponse D2 (Prob(ω=3%))
Réponse D3 (Espérance n(ω=8%))
Réponse D4 (Espérance n(ω=8%))
Cet exercice nous permet d'introduire les notions de "risque de l'acheteur", qui est le risque d'accepter à tort un lot défectueux ; et de "risque du fournisseur", qui est le risque de se voir refuser un lot acceptable.
Les critères de l'acheteur et du fournisseur n'étant pas les mêmes, il convient d'établir un test de réception le plus équitable possible. Les tests étant parfois destructifs, il convient également de veiller à prélever le moins de pièces possible.
Exercice 3
Un fabricant produit des axes cylindriques dont le diamètre est distribué suivant une loi normale d'écart-type égal à 8.
Les limites de tolérance pour le diamètre sont [90, 130]. Pour réceptionner un lot important de ces pièces, on décide d'adopter soit un procédé quantitatif A, soit un procédé qualitatif B.
Comparer les deux procédés.
Procédé A : On prélève n pièces, on mesure leurs diamètres et on calcule la moyenne m des n diamètres, puis on adopte la règle suivante :
- si a < m < b, on accepte le lot.
- si m < a ou m > b, on le refuse.
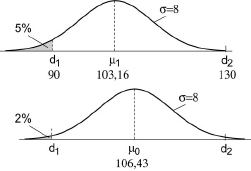
On détermine n, a et b en s'imposant les conditions :
- si la proportion de pièces défectueuses dans le lot (diamètre extérieur à l'intervalle [90, 130]) est supérieure à 5 %, on veut avoir 96 % de chance au moins de refuser le lot ;
- si cette proportion est inférieure à 2 %, on veut avoir 15 % de chance au plus de refuser le lot.
Procédé B : On prélève 300 pièces, on les passe au calibre et on compte le nombre k de pièces défectueuses, puis on adopte la règle suivante :
- si k <= 8, on accepte le lot ;
- si k > 8, on le refuse.
Commencez par calculer la proportion de déchets lorsque l'appareil est bien réglé. Vous constaterez que cette valeur est faible (1.24 %) ; ceci signifie que pour atteindre 2% puis 5% de déchets il faut décaler le réglage vers la droite ou vers la gauche de sorte que la proportion de déchets du côté opposé à celui vers lequel on dérègle la machine deviennent négligeable. N'hésitez pas à faire des schémas, ils vous faciliteront grandement la tache.
Exercice 4
Dans un atelier de peinture, l’air est analysé toutes les heures. Le seuil maximal admissible pour un certain polluant est fixé à 7,7 ppm. Si la teneur du polluant est distribuée suivant une loi normale de moyenne 7,6 et d’écart-type 0,04 et si l’erreur de mesure suit une loi normale de moyenne 0 et d’écart-type 0.03 calculer les probabilités pour que :
- Une mesure dépasse 7,7.
- La moyenne de 2 mesures dépasse 7,7.
Réponse A
Réponse B
On vous dit ici que la moyenne de l'erreur de mesure est nulle. D'un point de vue un peu plus "technique", on dit qu'il n'y a pas d'erreur systématique. L'exercice ne présente pas difficulté particulière, si ce n'est que l'on traite plusieurs variable aléatoire (la teneur en polluant et l'erreur de mesure).
Exercice 5
Pour réceptionner un lot d'acier, on se propose d'examiner sa résistance à la traction. Pour cela, on prélève dans le lot des éprouvettes cylindriques qui sont soumises à un effort de traction jusqu'à rupture.
En admettant que l'ensemble des éprouvettes que l'on pourrait extraire donnerait lieu, en ce qui concerne leur résistance, à une distribution normale d'écart-type égal à 20 kg/mm², on se propose d'élaborer une règle de contrôle satisfaisant aux conditions suivantes. On prélèvera un nombre fixé n d'éprouvettes et on déterminera la moyenne m de leurs résistances. Le lot sera accepté (ou refusé) selon que m sera supérieure (ou inférieure) à une certaine valeur x.
Déterminer n et x de telle façon que :
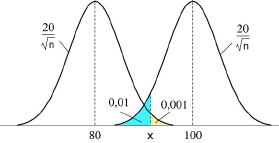
- - si la résistance moyenne du lot est égale (ou inférieure) à 80 kg/mm², la probabilité α qu'il soit accepté est égale (ou inférieure) à 0.001;
- - si la résistance moyenne du lot est égale (ou supérieure) à 100 kg/mm², la probabilité β qu'il soit refusé est égale (ou inférieure) à 0.01.
Quelle est, en fonction de la résistance moyenne du lot, la probabilité pour que le lot soit accepté après un tel jugement sur échantillon ?
Quelle signification concrète peut-on donner à α et β du point de vue de l'acheteur et de celui du fournisseur ?
Cet exercice permet de mettre en application les notions de "risque de l'acheteur" α et de "risque du fournisseur" β. On vous propose de mettre en place un test de réception répondant aux critères de l'acheteur et du fournisseur. La résolution de l'exercice est grandement facilitée si vous prenez le temps de faire un schéma clair, faisant figurer les différents paramètres du problème.
Une fois cela effectué, vous trouverez sans difficulté le système d'équations à résoudre.
Mise en garde : faites bien attention à différencier la population de départ qui suit une loi normale et la population de n éprouvettes dont on va s'intéresser à la loi de la moyenne ...
Exercice 6
Un lot d’un certain type de fusées a été stocké pendant deux ans. Les spécifications de ce lot indiquent une portée en moyenne égale à 2000 mètres avec un écart-type de 100 mètres.
On veut contrôler si le lot est encore en état. On fixe pour cela que :
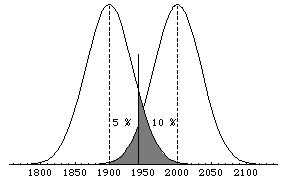
- la probabilité de réformer le lot si la portée moyenne a diminué de 100 mètres doit être égale à 90%,
- la probabilité de le réformer si elle n’a pas changé doit être égale à 5% seulement.
- Combien de fusées faut-il contrôler ?
- Si la moyenne de l’échantillon contrôlé est trouvée égale à 1930 mètres, doit-on réformer le lot ?
Réponse A
Cet exercice est en tout point similaire à l'exercice 5. Il permet de mettre en application les notions de "risque de l'acheteur" α et de "risque du fournisseur" β. On vous propose de mettre en place un test de réception répondant aux critères de l'acheteur et du fournisseur.
La résolution de l'exercice est grandement facilitée si vous prenez le temps de faire un schéma clair, faisant figurer les différents paramètres du problème. Une fois cela effectué, vous trouverez sans difficulté le système d'équations à résoudre.
Mise en garde : faites bien attention à différencier la population de départ qui suit une loi normale et la population de n éprouvettes dont on va s'intéresser à la loi de la moyenne...