
La Loi Normale
L'objectif du chapitre est de présenter la loi normale qui est le modèle probabiliste le plus utilisé pour décrire de très nombreux phénomènes observés dans la pratique. Une grande attention devra être accordée aux concepts, essentiels en statistiques, d'espérance mathématique et de variance et aux opérations qui leurs sont attachées.
1 - Variables Aléatoires Continues
Loi De Probabilité
Rappelons que si, à un ensemble de possibilités Ω, nous attachons un nombre X prenant les valeurs : x1, ..., xi, ..., xn, lorsque se produit l'un des événements : e1, ..., ei, ..., en, on dit que X est une variable aléatoire. Cette variable est définie lorsqu'on connait les probabilités :
p(x1), ..., p(xi), ..., p(xn)
correspondant aux valeurs possibles de X. Ces probabilités sont obligatoirement telles que :
p(x1) + ... + p(xi) + ... + p(xn) = 1
et la correspondance { xi, p(xi)} est appelée : loi de probabilité (ou distribution de probabilité) de la variable aléatoire X.
Si les valeurs possibles de X, sont réparties de façon continue sur un intervalle fini ou infini, X est une variable aléatoire continue. Une telle variable est définie si l'on connait la probabilité pour que X prenne une valeur dans tout intervalle [ x, x + h [. On se donne pour cela la fonction de répartition de X :
P(x) = Prob{X < x}
qui permet de calculer, pour tout intervalle :
Prob{x ≤ X< x + h} = P(x+h) - P(x)
Un cas particulier important, auquel nous nous attacherons exclusivement dans ce qui suit, est celui où la fonction de répartition est continue, et peut être mise sous la forme :
P(x)= ∫-∞x p(u) du
où p(x) s'appelle la densité de probabilité de X, appellation qui résulte du fait que :
p(x) = lim Δ x → 0 Prob { x ≤ X < x + Δx } Δx
La densité de probabilité p(x) ou la fonction de répartition P(x) définissent la loi de probabilité d'une variable aléatoire continue X. Elles donnent lieu aux représentations graphiques suivantes :
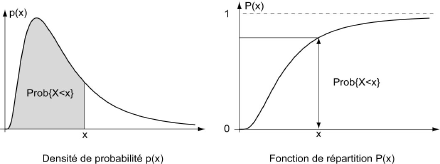
Il est important de bien noter que, conformément aux axiomes qui définissent les probabilités :
∫-∞+∞ p(x).dx = 1 et 0 ≤ P(x) ≤ 1
Loi Uniforme
La variable aléatoire U est distribuée uniformément sur l'intervalle [a, b] si sa densité de probabilité est constante sur cet intervalle :
p(u) = 1/(b-a)
et si sa fonction de répartition a, par conséquent, l'équation suivante :
P(u) = (u-a)/(b-a)
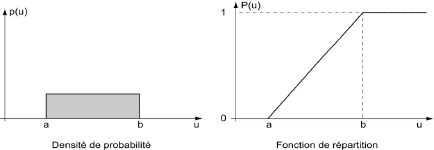
Loi Exponentielle
Nous avons montré dans le chapitre précédent que, si la probabilité d'apparition d'un événement pendant un intervalle de temps Δt était égale à λ.Δt, la probabilité pour qu'il se produise k fois pendant un intervalle de temps t, était donnée par la loi de Poisson de paramètre λt :
pk(t)= (λt)k.e-λt / k!
Si, maintenant, on considère les intervalles de temps T qui s'écoulent entre les événements successifs d'un processus de Poisson, soit F(t) la fonction de répartition de T. On a :
F(t) = 1 - Prob{T>t}
Or cette dernière probabilité est égale à la probabilité pour qu'il ne se produise aucun événement jusqu'à l'instant t, c'est-à-dire p0(t), et par conséquent :
F(t) = 1 - e-λt
C'est la loi exponentielle qui peut constituer un modèle intéressant pour les durées de vie aléatoires de certains matériels (tubes électroniques) : à chaque instant t de la vie du matériel, la probabilité de défaillance pendant l'intervalle de temps Δt qui suit, est indépendante de t et égale à λ.Δt.
Loi De Probabilité À Deux Dimensions
Si, à un événement aléatoire, sont attachés deux nombres X et Y, ces deux nombres définissent un vecteur aléatoire à deux dimensions. La loi de probabilité d'un tel vecteur peut être définie par la fonction de répartition :
P(x,y) = Prob{X<x, Y<y}
où la virgule se lit "et". Si cette fonction est dérivable en x et y, on peut définir la densité de probabilité p(x,y) qui est telle que :
p(x,y) dx dy = Prob{x≤X<x+dx, y≤Y<y+dy}
Géométriquement p(x,y) dx dy peut s'interpréter comme la probabilité pour que l'extrémité du vecteur aléatoire (X,Y) se trouve dans une aire ds = dx.dy autour du point (x, y). S'intéressant à la variable X, par exemple, indépendamment de la variable Y, on obtient la distribution marginale de X en calculant sa densité de probabilité p1(x) :
p1(x) dx = Prob{x≤X<x+dx} = dx ∫-∞+∞ p(x,y) dy
De même la distribution marginale de Y est définie par la densité de probabilité p2(x) :
p2(y) dy = Prob{y≤Y<y+dy} = dy ∫-∞+∞ p(x,y) dx
Indépendance De Deux Variables Aléatoires
Par définition, deux variables aléatoires sont indépendantes si la probabilité pour que la valeur de l'une d'elle tombe dans un intervalle donné, ne dépend pas de la valeur prise par l'autre. La probabilité conditionnelle de X, par exemple, est donc indépendante de Y. Or elle s'écrit, avec les notations ci-dessus :
Prob{x≤X<x+dx/y≤Y<y+dy} = p(x,y) dx dy / p2(y) dy = p(x,y) dx / p2(y)
Si les deux variables sont indépendantes, cette expression doit dépendre de x seulement et l'on doit donc pouvoir faire disparaître p2(y) par simplification. De la même façon, l'expression :
Prob{y≤Y<y+dy/x≤X<x+dx} = p(x,y) dy / p1(x)
doit dépendre de y seulement et l'on doit pouvoir la simplifier pour faire disparaître p1(y). Il en résulte que p(x,y) doit être égal au produit des densités de probabilité marginales de X et de Y :
p(x,y) = p1(x) p2(y)
Cette condition est évidemment nécessaire et suffisante. Elle se généralise pour un nombre quelconque de variables aléatoires indépendantes dans leur ensemble.
Fonctions De Variables Aléatoires
Etant données une variable aléatoire X, définie par sa densité de probabilité p(x), et une fonction f, la variable aléatoire f(X), fonction de la variable aléatoire X, est définie de la façon suivante : f(X) prend la valeur f(x), lorsque X prend la valeur x.
On remarquera qu'une variable f(X) peut prendre la même valeur pour deux valeurs différentes xi et xj de X. La probabilité de la valeur f(xi) ou f(xj) est alors égale à p(xi) + p(xj).
On peut aussi définir des fonctions de plusieurs variables aléatoires. La somme de deux variables aléatoires, notamment, se définit de la façon suivante : étant donné deux variables aléatoires X et Y, leur somme est la variable aléatoire (X+Y) qui prend la valeur (x+y) lorsque X prend la valeur x et Y prend la valeur y. Là encore, une même valeur de la somme peut être obtenue pour deux couples différents de valeurs de X et Y. Penser, par exemple à la variable : on jette deux dés et on en fait la somme.
2 - Espérance
Espérance et Moments d'une Variable Aléatoire
Etant données une variable aléatoire X définie par sa densité de probabilité p(x) et une fonction f, on désigne par le terme d'espérance mathématique de la variable aléatoire f(X), et on la note E[f(X)], l'expression :
E[f(X)]= ∫-∞+∞ f(x)p(x)dx
C'est donc un opérateur qui transforme la variable aléatoire f(X) en un nombre. Appliqué à la variable X elle-même, l'opérateur donne sa moyenne μ :
μ=E(X)= ∫-∞+∞ x p(x)dx
Dans le cas d'une variable aléatoire discrète à valeurs positives ou nulles : x0 ,... , xi ,... , xn , l'expression précédente devient :
μ = E[f(X)] = ∑i=0n f(xi)p(xi)
et toutes les propriétés de l'opérateur E que nous démontrerons par la suite, pour une variable continue, s'étendent sans difficulté au cas d'une variable discrète.
Lorsque f(X) est une puissance de X, l'expression E(Xk) est appelée moment d'ordre k de la variable aléatoire X. La moyenne μ = E(X) est ainsi le moment d'ordre 1 de la variable X. Elle s'interprète comme l'abscisse du centre de gravité de la distribution de probabilité et c'est, à ce titre, une caractéristique de tendance centrale de la distribution : les valeurs d'une variable aléatoire se répartissent autour de sa moyenne.
Variance et Écart-Type
Il peut alors s'avérer intéressant de rapporter une variable aléatoire à sa moyenne, autrement dit de la centrer. On obtient alors le moment centré d'ordre k :
E[(X-μ)k] = ∫-∞+∞ (x-μ)k p(x)dx
Le moment centré d'ordre 2 est appelé variance et il revêt une importance toute particulière. Nous le noterons σ²(X), ou très souvent σ²:
σ²(X) = E[(X-μ)²] = ∫-∞+∞ (x-μ)² p(x)dx
Par analogie avec la mécanique, on peut dire que μ est le centre de gravité et que σ² est le moment d'inertie de la distribution. Sa racine carrée σ est appelée l'écart-type, qui s'interprète comme une mesure de la dispersion d'une variable aléatoire : plus les valeurs de la variable sont susceptibles de s'éloigner de sa moyenne, plus son écart-type est grand. C'est ce que montre l'inégalité de Bienaymé-Tchebichef.
Inégalité de Bienaymé-Tchebichef
Soit X une variable aléatoire de moyenne μ et d'écart-type σ, mais à ceci près quelconque. La probabilité pour qu'elle prenne une valeur à l'extérieur d'un intervalle [μ-a, μ+a], où a est un nombre positif, est donnée par l'intégrale :
Prob{|X-μ|>a}= ∫❘X-μ❘ > a p(x)dx
Pour les valeurs x extérieures à l'intervalle [μ-a, μ+a], (x-μ)² est supérieur à a² , et l'on a, par conséquent :
Prob{|X-μ|>a}< 1/a² ∫❘X-μ❘ > a (x-μ)² p(x)dx
On majore encore l'intégrale en intégrant, pas seulement pour |x-μ| > a, mais de -∞ à +∞. On obtient ainsi :
Prob{|X-μ|>a}< 1/a² ∫-∞+∞ (x-μ)² p(x)dx
c'est à dire :
Prob{|X-μ|>a}< σ²/a²
C'est l'inégalité de Bienaymé-Tchebichef qui s'interpréte ainsi : plus σ est petit, plus les grandes valeurs de |X-μ| sont improbables, donc moins la variable X est dispersée autour de sa moyenne μ.
Si l'on pose a = t σ, l'inégalité s'écrit :
Prob{|X-μ|>t σ}< 1/t²
et exprime que la probabilité pour que X s'éloigne de sa moyenne de plus que t fois son écart-type σ, est inférieure à 1/t². Il y a, en particulier, moins de 1 chance sur 4 pour que X s'éloigne de μ de plus de 2 fois σ, et il est très improbable (probabilité inférieure à 1/100 ) que X s'éloigne de μ de plus de 10 fois σ.
Ces résultats sont très généraux puisqu'ils ne nécessitent aucune hypothèse sur la forme de la loi de probabilité de X. On peut, bien sûr, les rendre beaucoup plus précis et les serrer davantage dans chaque cas particulier où la loi de probabilité de X est connue.
Linéarité de l'opérateur Espérance
On montre très facilement que, a et b étant deux constantes, on a :
E(aX+b) = a E(X) + b.
Soient maintenant deux variables X et Y définies par leur densité de probabilité p(x, y). L'espérance mathématique de leur somme s'écrit :
E(X+Y) = ∫-∞+∞ ∫-∞+∞ (x+y) p(x,y) dx dy
E(X+Y) = ∫-∞+∞ x dx ∫-∞+∞ p(x,y) dy + ∫-∞+∞ y dy ∫-∞+∞ p(x,y) dx
E(X+Y) = ∫-∞+∞ x p1(x) dx + ∫-∞+∞ y p2(y) dy
E(X+Y) = E(X) + E(Y)
Cette propriété s'applique, bien entendu, à la somme d'un nombre quelconque de variables. On notera, d'autre part, que la démonstration n'a requis aucune hypothèse sur l'indépendance des variables aléatoires considérées.
Calculs de Variances de Variables Aléatoires
Rappelons qu'étant donnée une variable aléatoire de moyenne μ, sa variance s'écrit :
σ²(X) = E[(X-μ)²].
De la forme même de la variance, il résulte que :
- la variance d'une constante est égale à 0,
- dans un changement d'échelle de rapport k, la variance est multipliée par k².
Si, d'autre part, on développe l'expression de la variance, et qu'on utilise les propriétés de linéarité de l'espérance, il vient :
σ²(X) = E(X² - 2μX + μ²) = E(X²) - 2μ E(X)+ μ²
et, puisque E(X) = μ :
σ²(X) = E(X²) - μ²
Cette relation sera très souvent utilisée. On la retiendra facilement en écrivant que :
σ²(X) = E(X²) - E(X)²
et en énonçant que : la variance est égale à l'espérance du carré moins le carré de l'espérance. Appliquons la à quelques-unes des variables aléatoires déjà rencontrées.
- Loi uniforme
Soit la variable U distribuée uniformément sur l'intervalle [0, a]. Elle a pour densité de probabilité 1/a , donc pour moyenne :
E(U) = ∫0a x 1/a dx = a/2pour moment d'ordre 2 :
E(U²) = ∫0a x² 1/a dx = a²/3et, enfin, pour variance :
σ²(U) = E(U²) - E(U)² = a²/12
- Variable de Bernouilli
Les moments d'ordres 1 et 2 sont égaux :
E(X) = E(X²) = 1.ϖ + 0.(1-ϖ) = ϖ
La variance est donc égale à :
σ²(X) = E(X²) - E(X)² = ϖ-ϖ² = ϖ(1 - ϖ)
- Loi de Poisson
La loi de Poisson est définie par la densité de probabilité :
p(k) = e-λ λk/k!
et nous avons déjà calculé sa moyenne :
E(K) = ∑k=0∞ k e-λ λk/k! = λ ∑k=0∞ e-λ λk-1/(k-1)! = λ
Pour trouver sa variance, calculons d'abord :
E[K(K-1)]= ∑k=0∞ k(k-1) e-λ λk/k! = λ²E[K(K-1)] = E(K²) - E(K) = λ²
E(K²)= λ² + λ
σ²(K) = E(K²) - E(K)² = λ² + λ - λ² = λ
La loi de Poisson est donc telle que moyenne et variance soient toutes les deux égales à λ.
- Loi exponentielle
La densité de probabilité est :
p(t) = λe-λt
En intégrant par parties, on trouve pour la moyenne :
E(T) = ∫0∞ t λe-λtdt = 1/λpuis, pour le moment d'ordre 2 :
E(T²)= ∫0∞ t² λe-λt dt = 2/λ²ce qui montre que l'écart-type est égal à la moyenne :
σ²(T)= 2/λ² - 1/λ² = 1/λ²
Indépendance et Covariance de Deux Variables Aléatoires
Soient X et Y deux variables aléatoires définies par leur densité de probabilité p(x,y). L'espérance mathématique du produit de ces deux variables est, par définition :
E(X Y) = ∫-∞+∞ ∫-∞+∞ x y p(x,y)dx dy
Si les deux variables aléatoires sont indépendantes :
p(x, y) = p1(x) p2(y)
et, par suite :
E(X Y) = ∫-∞+∞ x p1(x)dx ∫-∞+∞ y p2(y)dy = E(X) E(Y)
Il s'agit là d'un théorème très important qui peut s'énoncer de la façon suivante : si deux variables aléatoires sont indépendantes, l'espérance de leur produit est égale au produit de leurs espérances
.
Ce théorème justifie la définition d'une quantité appelée la covariance de X et Y :
σ(X,Y) = E(X Y) - E(X)E(Y)
qui a la propriété suivante : la covariance de deux variables aléatoires indépendantes est nulle. Il faut faire attention au fait que la réciproque n'est pas vraie, en général.
Variance D'une Somme (ou d'une Différence) de Variables Aléatoires Indépendantes
Soient X et Y deux variables aléatoires. La variance de leur somme (ou de leur différence) peut s'écrire (espérance du carré moins carré de l'espérance) :
σ²(X±Y) = E[(X±Y)²] - E(X±Y)²
Le premier terme du second membre se développe en :
E[(X±Y)²] = E(X²) ± 2E(X Y)+E(Y²)
et le second terme en :
E(X±Y)² = E(X)² ± 2E(X)E(Y)+ E(Y)²
On a donc, en réorganisant les termes :
σ²(X±Y) = (E(X²) - E(X)²) ± 2(E(X Y)-E(X)E(Y)) + (E(Y²)-E(Y)²)
où l'on reconnait :
σ²(X±Y) = σ²(X) ± 2σ(X,Y) + σ²(Y)
Si, maintenant, les deux variables X et Y sont indépendantes, leur covariance est nulle, et :
σ²(X±Y) = σ²(X)+ σ²(Y)
propriété qui s'énonce ainsi : la variance de la somme ou de la différence de deux variables aléatoires indépendantes est égale à la somme de leurs variances.
3 - La Loi Normale
Définition et Propriétés
La loi de probabilité la plus utilisée en statistique est la loi normale, encore appelée loi de Gauss, ou de Laplace-Gauss. Une variable aléatoire X suit une loi normale si sa densité de probabilité a pour équation :
p(x) = 1/(σ.√(2π)) . e-1/2 ((x-μ)/σ)²
dont le graphe est la fameuse "courbe en cloche", et qui dépend de deux paramètres μ et σ qui ne sont autres, comme on le montrera au paragraphe suivant, que la moyenne et l'écart-type de X.
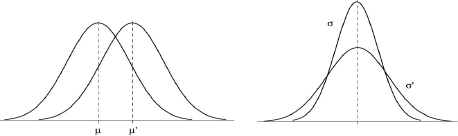
La distribution est symétrique par rapport à μ qui caractérise donc la tendance centrale. Quant à σ, il caractérise la dispersion de la distribution. Plus il est grand, plus la distribution est étalée de part et d'autre de μ. Les points d'inflexion se trouvent à (μ-σ) et (μ+σ), avec :
Prob{|X-μ| < σ} = 68,26 %
Il sera bon de conserver en mémoire deux autres valeurs intéressantes :
Prob{|X-μ| > 1,96 σ} = 5%
Prob{|X-μ| > 2,58 σ} = 1%
que l'on pourra aussi comparer à celles que donnait l'approximation de Bienaymé-Tchebichef pour une loi de probabilité quelconque.
Calcul de la Moyenne et de la Variance
Nous allons montrer que la moyenne d'une variable qui suit une loi normale est égale à μ, et que sa variance est égale à σ² . La démonstration est uniquement calculatoire et pourra être omise.
La moyenne est, par définition, égale à :
E(X) = 1/(σ.√(2π)) ∫-∞+∞ x e-1/2 ((x-μ)/σ)² dx
Pour calculer cette intégrale, faisons le changement de variable, classique pour les calculs sur la loi normale :
u = (x-μ)/σ
Il vient :
E(X) = 1/√(2π) ∫-∞+∞ (μ+σ u) e-u²/2 du
E(X) = μ/√(2π) ∫-∞+∞ e-u²/2 du + σ/√(2π)∫-∞+∞ u e-u²/2 du
La seconde intégrale est nulle. Quant à la première, elle est égale à √(2π) , ce qui se montre en posant :
I = ∫-∞+∞ e-u²/2 du
I² = ∫-∞+∞ ∫-∞+∞ e-1/2 (x² + y²) dxdy
que l'on intègre facilement en passant en coordonnées polaires. D'où finalement :
E(X) = μ
De la même façon :
E[(X-μ)²] = 1/(σ.√(2π)) ∫-∞+∞ ( x - μ )² e-1/2 (x-μ)² dx
qui devient, après changement de variable :
E[(X-μ)²] = σ²/√(2π) ∫-∞+∞ u² e-u²/2 du
L'intégrale se calcule par parties, et il vient :
E[(X-μ)²] = σ²
La Loi Normale Réduite
Etant donnée une variable suivant une loi normale de moyenne μ et d'écart-type σ, sa densité de probabilité est telle que :
p(x)dx = 1/(σ.√(2π)) e-1/2 ((x-μ)/σ)² dx
Faisant le changement de variable : U = (X-μ)/σ , on peut écrire : du = dx/σ , d'où :
p(u)du = 1/√(2π) e-u²/2 du
La nouvelle variable suit donc une loi normale qui est dite centrée (E(U)=0) et réduite ( σ²(U)=1), et qui ne fait intervenir aucun paramètre.
Cette loi, appelée loi normale réduite, est tabulée. Les tables donnent généralement, pour différentes valeurs de u, les probabilités :
Prob{-∞ < U < u} = P(u) = 1/√(2π) ∫-∞u e-t²/2 dt
qui, compte tenu de la symétrie de la loi et de l'additivité des probabilités pour des intervalles disjoints, permettent de connaître la probabilité attachée à n'importe quel intervalle.
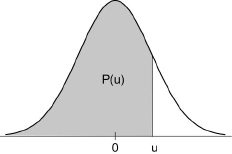
On en déduit facilement la probabilité pour qu'une variable suivant une loi normale quelconque X(μ, σ) de moyenne μ et d'écart-type σ, soit comprise dans un intervalle donné [x1, x2] :
Prob{x1 < X < x2} = Prob{(x1-μ)/σ < U < (x2-μ)/σ}
Fonctions Linéaires de Variables Normales
Etant données deux variables X1 et X2 indépendantes et suivant toutes les deux des lois normales, et deux constantes a1 et a2 , on peut montrer que la fonction linéaire (a1 X1 + a2 X2) suit elle-même une loi normale. Pour spécifier cette loi, il faut connaître sa moyenne et sa variance. Les propriétés générales (c'est-à-dire indépendantes des lois de probabilité en jeu) des opérateurs espérance et variance permettent d'établir que :
E(a1 X1 + a2 X2) = a1 E(X1) + a2 E(X2)
et que :
σ²(a1 X1 + a2 X2) = a1² σ²(X1)+ a2² σ²(X2)
Cette propriété s'étend évidemment à une fonction linéaire d'un nombre quelconque de variables indépendantes suivant des lois normales.
Théorème Central Limite
Ce théorème établit une propriété encore plus générale que la précédente, et qui va justifier l'importance considérable de la loi normale, à la fois comme modèle pour décrire des situations pratiques, mais aussi comme outil théorique. Il s'énonce ainsi :
Soit X1,..., Xi,..., Xn, une suite de n variables aléatoires indépendantes, de moyennes μ1,..., μi,..., μn, et de variances σ1²,..., σi²,..., σn², et de lois de probabilité quelconques, leur somme suit une loi qui, lorsque n augmente, tend vers une loi normale de moyenne μ = ∑i=1n μi et de variance σ² = ∑i=1 n σi². Il y a une seule condition restrictive, c'est que les variances soient finies et qu'aucune ne soit prépondérante devant les autres.
La loi normale comme modèle
Prenons l'exemple du fonctionnement d'un tour. Le réglage du tour a pour but d'obtenir des pièces présentant une cote bien définie ; mais on sait que de multiples causes perturbatrices agissent au cours de l'usinage d'une pièce : vibrations, usures, variations de courant ... Or si les causes perturbatrices sont nombreuses, si leurs effets interviennent de façon additive, enfin si la dispersion provoquée par chacune d'elles reste faible par rapport à la dispersion totale, alors le théorème central limite signifie qu'on doit observer une fluctuation globale très voisine de la loi normale. Et, comme ce mécanisme d'intervention de causes perturbatrices est très répandu dans la nature, il en résulte que la loi normale occupe en statistique une place privilégiée.
Limite de la loi binomiale
On a défini une variable de Bernouilli comme une variable qui prend la valeur 1 avec la probabilité ϖ, et la valeur 0 avec la probabilité (1-ϖ), et montré que sa moyenne est égale à ϖ et sa variance à ϖ(1-ϖ). Or on peut considérer une variable binomiale comme la somme K n de n variables de Bernouilli. Il résulte du théorème central limite que, si n est suffisamment grand (en pratique à partir de n=50), la loi binomiale peut être approximée par une loi normale de moyenne n ϖ et de variance n ϖ(1-ϖ). C'est pourquoi les tables de la loi binomiale s'arrêtent généralement à n=50.
La Loi Log-Normale
On appelle loi log-normale une loi qu'une transformation du type log(X-x0) ramène à une loi normale. Cette loi est très répandue, notamment dans le domaine des sciences naturelles (géologie, biologie, ...) et des sciences humaines (psychologie, économie, ...). Chaque fois que les causes perturbatrices à l'origine des fluctuations observées répondent aux conditions du théorème central limite mais sont multiplicatives, on enregistre des distributions modélisables par des lois log-normales.
Exercices
Vous pouvez entrer la réponse sous forme décimale (1.33), fractionnaire (4/3), ou encore passer une expression numérique: (5.5+2.5)/3/2
Il y a une tolérance sur la réponse de 0.001. Soyez précis, et ne confondez pas probabilité et pourcentage !
Exercice 1
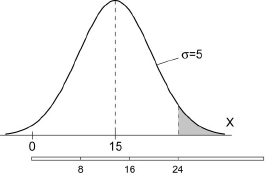
Le profilé laminé à partir d'un lingot est découpé en billettes de 8 mètres de longueur. L'extrémité du profilé correspondant au laminage de la tête du lingot présente un défaut sur une certaine longueur X qui suit une loi normale de moyenne égale à 15 mètres et d'écart-type égal à 5 mètres.
- Pour tenter d'éliminer la longueur atteinte, on déclasse systématiquement les trois billettes de tête. Quel est le risque pour que la quatrième billette présente encore un défaut ?
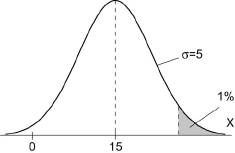
- Calculer le nombre de billettes à déclasser pour que la première billette retenue soit propre avec un risque inférieur à 1 %.
Réponse A
Réponse B
Il est important ici de bien comprendre que le défaut est continu (par exemple une retassure). Ainsi, si la 3ème billette est éliminée, la première et la deuxième le sont aussi.
Exercice 2
On usine des axes sur un tour automatique. L'intervalle de tolérance sur le diamètre de ces axes est (355, 365) en centièmes. Les diamètres des axes usinés sur la machine sont distribués suivant une loi normale de moyenne correspondant au réglage de la machine et d'écart-type 2 centièmes.
- Montrer que le meilleur réglage est 360.
- Quelle est alors la proportion de déchets ?
- Quelle est la proportion de déchets si la machine se dérègle et que la moyenne devient égale à 358 ?
Réponse A
Cf. Solution
Réponse B
Réponse C
On vous demande ici de montrer que le meilleur réglage est le milieu de l'intervalle de tolérance. Ce résultat important sera réutilisé plus tard, retenez-le donc. Il existe deux approches pour démontrer cela :
-La première est purement calculatoire : commencez par écrire la proportion de déchets en fonction de la moyenne de fabrication μ , puis cherchez pour quelle valeur de μ cette proportion est minimale. Avant de vous lancer dans des calculs compliqués, réfléchissez un peu...
-La seconde est graphique et consiste à montrer simplement que, partant du réglage optimale, si on dérègle μ, alors la proportion de déchets augmente.
Exercice 3
La durée de vie d'un certain type de lampes à incandescence suit une loi normale de moyenne égale à 160 heures. Les spécifications impliquent que 80 % au moins de la production tombe entre 120 et 200 heures. Quel est le plus grand écart-type acceptable pour que la fabrication réponde aux spécifications ?
Réponse
Il s'agit ici d'un problème très simple. La seule difficulté réside dans la bonne compréhension de l'énoncé. Que signifie : 80 % au moins de la production doit tomber entre 120 et 200 heures ?
-> on ne veut pas excéder 20 % de rebus, sachant qu'est considérée comme défectueuse toute ampoule dont la durée de vie est inférieure à 120 h ou supérieure à 200 h.
-> on ne veut donc pas excéder 10 % de rebus à gauche (<120h), et 10 % de rebus à droite (>200h).
Exercice 4
Il existe deux méthodes pour doser le phosphore dans l'acier d'une coulée :
- méthode C : dosage par voie chimique,
- méthode S : dosage par méthode spectrographique.
Pour toutes les coulées effectuées pendant une certaine période, on a réalisé les deux mesures et calculé la variance σ²(X) des mesures obtenues par la méthode C, la variance σ²(Y) des mesures obtenues par la méthode S, et la variance σ²(X-Y) des différences entre les mesures relatives à une même coulée. On a trouvé : σ²(X)=20, σ²(Y)=35 et σ²(X-Y)=50.
Quelle est la variance de la vraie teneur en phosphore pendant la période considérée ? Quelles sont les variances caractérisant les erreurs de mesure commises par les méthodes C et S ? Quelle est la covariance entre les deux mesures ?
On admettra que le résultat d'une mesure est la somme de la vraie teneur en phosphore et d'une erreur indépendante de cette teneur (modèle de l'erreur "absolue").
σc²
σs²
σp²
σXY²
Commencez par adopter des notations claires, puis traduisez mathématiquement le modèle de l'erreur absolue :
- soit P la vraie valeur en phosphore
- soit εc l'erreur par voie chimique
- soit εs l'erreur par voie spectrographique
Faites également l'hypothèse que les appareils sont bien réglés et qu'ils n'introduisent donc pas d'erreur systématique, càd que E(εc)=E(εs)=0. Sous ces conditions,
- le résultat d'une mesure chimique est : X = P + εc
- le résultat d'une mesure par spectrographie est : Y = P + εs
Vous avez maintenant tout ce qu'il faut pour pouvoir caractériser la précision des deux méthodes de mesures (σc² et σs²) ainsi que la variabilité de la fabrication (σp²).
Exercice 5
A une heure déterminée, soit Z le nombre de voyageurs arrivant à une station dans une voiture de métro. On compte le nombre X de voyageurs qui montent et le nombre Y de voyageurs qui descendent. La voiture repart avec N personnes. On admettra que les variables X, Y, et Z sont indépendantes et qu'elles suivent des lois normales de moyennes E(X)= 40, E(Y)=30, E(Z)=100 et d'écart-type : σ(X)=9, σ(Y)=12 et σ(Z)=20.
Calculer la capacité n de la voiture pour que Prob{N > n} = 5 %.
Que pensez-vous de l'hypothèse d'indépendance des variables X,Y et Z ?
Exercice 6
Une étude a montré que, pour un haut-fourneau donné, lorsqu'on vise un poids de coulée μ Q , on obtient un poids de fonte distribué suivant une loi normale de moyenne justement égale au poids visé μ Q et d'écart-type σ Q tel que σ Q = γ μ Q où γ est le coefficient de variation du H.F. étudié. Les moyens de transport dont on dispose entre le H.F. et l'aciérie consistent en n poches identiques. Lorsqu'on cherche à remplir au maximum une poche, le poids de fonte contenue suit une loi normale de moyenne μ P et d'écart-type σ P.
Calculer le poids de coulée qu'il faut viser pour qu'au risque α près, on ne doive pas reboucher le H.F. non vide. Application numérique : γ = 0.01, n = 2, α = 10 %, μ P = 30T et σ P = 2 T.
Réponse
Cet exercice est particulièrement délicat. Commencez par identifier les différentes variables du problème.
Notez X la quantité de métal restant dans le haut fourneau, Q le poids de coulée, P1 la capacité de la première poche et P2 celle de la seconde.
Avant d'aller plus loin, interrogez-vous sur les éventuelles relations de dépendance entre ces variables. Si vous éprouvez des difficultés, n'hésitez pas à vous reporter au corrigé.
Identifier votre variable aléatoire et posez le problème.
Exercice 7
La production d'une taille (chantier de production du charbon), pendant le cycle d'abattage, est distribuée suivant une loi normale de moyenne 500 T et d'écart-type 50 T. Elle est desservie par un train de n berlines. Lorsqu'on cherche à remplir une berline, le poids chargé est distribué suivant une loi normale de moyenne 10 T et d'écart-type 1 T. Calculer n pour que le risque de "manque à vide" soit égal à 2 % seulement.
C'est exactement le même l'exercice 6 : le support est minier au lieu d'être sidérurgique.
Exercice 8
Un problème grave est posé en Lorraine par les effondrements d’anciennes exploitations souterraines du minerai de fer, qui menacent des villages construits à leur aplomb. Une des méthodes d’exploitation les plus courantes consistait à laisser en place, dans la couche exploitée, des piliers destinés à soutenir les terrains sus-jacents. Dans l’une de ces anciennes exploitations, les mesures ont montré que les contraintes dans les piliers suivaient une loi normale de moyenne égale à 10 bars et d’écart-type égal à 3 bars, que la résistance à la compression du minerai suivait une loi normale de moyenne égale à 50 bars et d’écart-type égal à 15 bars. On peut par ailleurs raisonnablement accepter l'indépendance entre contrainte et résistance. Quel est la probabilité de ruine d’un pilier ?
Réponse
Notez C la contrainte appliquée au pilier et R sa résistance. Dans quel cas y a-t-il ruine du pilier ? Identifier la variable d'étude et écrivez sa loi de probabilité.
Exercice 9
Des pièces de monnaie ont un poids distribué suivant une loi normale de moyenne 10 g et d'écart-type 0.15 g. Pour les compter, on les pèse par lots d'environ un kilo. Quel est le risque de faire une erreur d'une unité ?
Réponse
Commencez par raisonner avec un exemple concret: Si le poids mesuré est noté P, alors on estimera le nombre de pièces par l'entier le plus proche de n*=P/10.
Considérez que l'on dispose d'une centaine de pièces (n=100):
- Si P=1003 g alors n*=100.3 et n*=100
- Si P=1006 g alors n*=100.6 et n*=101 ; on commet donc une erreur de une unité.
Etendez ces constatations au cas général et concluez.
Exercice 10
Dans une tréfilerie, l'atelier pour l'émaillage du fil de cuivre comporte 4 machines. Chaque machine est alimentée à partir d'un stock reconstitué chaque jour.
- Sachant que la production journalière d'une machine suit une loi normale de moyenne 10 tonnes et d'écart-type 2 tonnes, calculer le stock pour que le risque de pénurie soit égal à 1 % seulement.
- Que devient le stock total qui serait nécessaire si l'on décidait d'organiser l'atelier de telle sorte que les 4 machines puissent être alimentées à partir d'un stock commun ?
Réponse A (en tonnes)
Réponse B (en tonnes)
Comme d'habitude, un petit schéma permet de fixer les idées. Dans quel cas y a-t-il rupture de stock ? Ne commencez pas les calculs avant d'avoir répondu à cette question.
Comparez les pertes journalières occasionnées par une pénurie dans le cas de stocks individuels et dans le cas d'un stock commun. Que concluez vous ?

![[Graphics:HTMLFiles/index_38.gif]](HTMLFiles/index_38.gif)
![[Graphics:HTMLFiles/index_39.gif]](HTMLFiles/index_39.gif)
![[Graphics:HTMLFiles/index_140.gif]](HTMLFiles/index_140.gif)
![[Graphics:HTMLFiles/index_210.gif]](HTMLFiles/index_210.gif)
![[Graphics:HTMLFiles/index_218.gif]](HTMLFiles/index_218.gif)
![[Graphics:HTMLFiles/index_226.gif]](HTMLFiles/index_226.gif)